Rebeca González Gálvez
ARITMÉTICA: NÚMEROS NATURALES
LICENCIATURA EN EDUCACIÓN PRIMARIA. ESTUDIE LA PREPARATORIA EN EL COLEGIO DE BACHILLERES DEL ESTADO DE MÉXICO PLANTEL 32 TOLUCA III. VIVO EN LA LOCALIDAD DE SAN ANDRES CRUXCONTITLAN TOLUACA,MÉXICO.
PRESENTACIÓN DEL CURSO






UNIDAD DE APRENDIZAJE I



La aritmética, su enseñanza y aprendizaje.
¿Qué estudia la aritmética?
La aritmética es el área del estudio de las matemáticas que se centra en tratar todo lo relacionado con los números, abordando lo que conocemos hasta hoy.
Las operaciones aritméticas son: suma, resta, multiplicación y división.
¿Qué son los números naturales?
En matemáticas un número natural es cualquiera de los números que se usan para contar los elementos de ciertos conjuntos, como también en operaciones de cálculo. Conjunto de signos que permiten expresar una cantidad con relación a su unidad.
Propósitos para la educación primaria
PROPÓSITO
| TIPO DE EJE TEMÁTICO | TEMA |
UTILIZAR | Número, algebra y variación. | Número, adición y sustracción, multiplicación y división |
IDENTIFICAR Y SIMBOLIZAR | Análisis de datos | Estadística y probabilidad |
USAR E INTERPRETAR | Forma, espacio y medida | Ubicación espacial Figuras y cuerpos geométricos Magnitudes y medidas |
CONOCER Y USAR | Número, algebra y variación y forma espacio y medida | Patrones, figuras geométricas Figuras y cuerpos geométricos |
CALCULAR Y ESTIMAR | Forma espacio y medida | Figuras y cuerpos geométricos Magnitudes y medidas |
BUSCAR, ORGANIZAR, ANALIZAR E INTERPRETAR | Análisis de datos | Estadística y probabilidad |
RECONOCER | Análisis de datos | Estadística y probabilidad |
Enfoque pedagógico:
La resolución de problemas en la educación básica es una meta de aprendizaje para aprender contenidos matemáticos
Orientaciones didácticas.
- Es conveniente averiguar como analizan la información que reciban de manera oral o escrita.
- Los alumnos proponen el camino a seguir.
- Trabajo en equipo.
- Manejo adecuado del tiempo.
- diversificar el tipo de problemas.
- Compartir experiencias con otros profesores.
Sugerencias de evaluación
- Reflexiona sobre sus propios avances.
- De los procedimientos informales a los procedimientos formales.
- De la justificación pragmática al uso de propiedades.
- De resolver problemas con ayuda a solucionar la autonomamente.
- La evaluación tiene un enfoque formativo por que se encuentra en procesos de aprendizaje, seguimiento al proceso de los alumnos.
- Líneas de progreso.
EVIDENCIAS PRIMERA UNIDAD
1. Preguntas del plan vigente para la educación básica
A)¿Cuáles son las características que determina el enfoque?
En la educación básica, la resolución de problemas es tanto una meta de aprendizaje como un medio para aprender contenidos matemáticos y fomentar el gusto con actitudes positivas hacia su estudio.
En el primer caso, se trata de que los estudiantes usen de manera flexible conceptos, técnicas, métodos o contenidos en general, aprendidos previamente; y en el segundo, los estudiantes desarrollan procedimientos de resolución que no necesariamente les han sido enseñados con anterioridad.
En ambos casos, los estudiantes analizan, comparan y obtienen conclusiones con ayuda del profesor; defienden sus ideas y aprenden a escuchar a los demás; relacionan lo que saben con nuevos conocimientos, de manera general; y le encuentran sentido y se interesan en las actividades que el profesor les plantea, es decir, disfrutan haciendo matemáticas
La resolución de problemas se hace a lo largo de la educación básica, aplicando contenidos y métodos pertinentes en cada nivel escolar, y transitando de planteamientos sencillos a problemas cada vez más complejos. Esta actividad incluye la modelación de situaciones y fenómenos, la cual no implica obtener una solución.
Es por ello que la evaluación no debe circunscribirse a la aplicación de exámenes en momentos fijos del curso, sino que debe ser un medio que permita al profesor y al estudiante conocer las fortalezas y debilidades surgidas en el proceso de aprendizaje Mediante actividades que utilizan herramientas tecnológicas es posible promover en los estudiantes la exploración de ideas y conceptos matemáticos, así como el análisis y modelación de fenómenos y situaciones problemáticas. Las herramientas de uso más frecuente en el diseño de actividades para el aprendizaje en matemáticas son las hojas electrónicas de cálculo, los manipuladores simbólicos y los graficadores
B) ¿Cuál es el campo de la formación que define las matemáticas en la educación?
Para su estudio, este espacio curricular se organiza en tres ejes temáticos y doce temas:
Número, álgebra y variación
Número
Adición y sustracción
Multiplicación y división
Proporcionalidad
Ecuaciones
Funciones
Patrones, figuras geométricas y expresiones equivalentes
Forma, espacio y medida
Ubicación espacial
Figuras y cuerpos geométricos
Magnitudes y medidas
Análisis de datos
Estadística
Probabilidad
C)¿Cuál es el perfil de egreso al termino de cada nivel educativo de acuerdo al ámbito de pensamiento matemático?
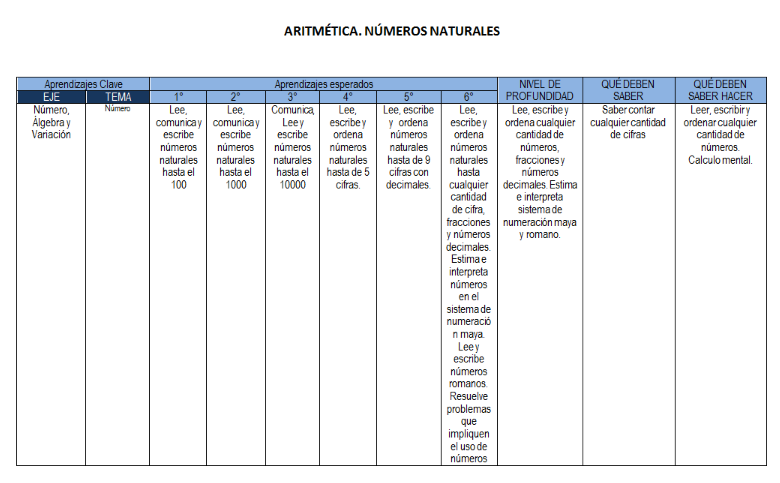
Aprendizajes esperados 1
- Lee, escribe y ordena números naturales hasta 100.
Comunica, lee, escribe y ordena números naturales hasta 1000
• Resuelve problemas de suma y resta con números naturales hasta 1000. Usa el algoritmo convencional para sumar.
• Calcula mentalmente sumas y restas de números de dos cifras, dobles de números de dos cifras y mitades de números pares menores que 100.
Resuelve problemas de multiplicación con números naturales menores que 10.
Aprendizaje esperado: 2
- Lee, escribe y ordena números naturales hasta 1000.
Aprendizajes esperados: 3
- Lee, escribe y ordena números naturales hasta 10000.
- Usa fracciones con denominador dos, cuatro y ocho para expresar relaciones parte-todo, medidas y resultados de repartos.
Aprendizajes esperados 4
- Lee, escribe y ordena números naturales hasta de cinco cifras...
- Usa fracciones con denominadores hasta 12 para expresar relaciones parte-todo, medidas, y resultados de repartos.
Aprendizajes esperados 5
- Lee, escribe y ordena números naturales hasta de nueve cifras y decimales.
- Ordena fracciones con denominadores múltiplos.
Aprendizajes esperados 6
- Lee, escribe y ordena números naturales de cualquier cantidad de cifras, fracciones y números decimales.
- Estima e interpreta números en el sistema de numeración maya.
- Lee y escribe números romanos.
- Resuelve problemas que impliquen el uso de números enteros al situarlos en la recta numérica, compararlos y ordenarlos.
2. PERFIL DE EGRESO POR NIVEL EDUCATIVO

3. PERFIL DE EGRESO EDUCACIÓN BÁSICA.
A) ¿Cuáles son los rasgos del perfil de egreso y los propósitos que propone el plan y programas para la educación básica?
R: 1) Se comunica con confianza y eficacia, Utiliza su lengua materna para comunicarse con eficacia, respeto y seguridad en distintos contextos con múltiples propósitos e interlocutores
2) Fortalece su pensamiento matemático, Amplía su conocimiento de técnicas y conceptos matemáticos para plantear y resolver problemas con distinto grado de complejidad, así como para modelar y analizar situaciones. Valora las cualidades del pensamiento matemático.
3) Gusta de explorar y comprender el mundo natural y social, Identifica una variedad de fenómenos del mundo natural y social, lee acerca de ellos, se informa en distintas fuentes, indaga aplicando principios del escepticismo informado, formula preguntas de complejidad creciente, realiza análisis y experimentos
4) Desarrolla el pensamiento crítico y resuelve problemas con creatividad, Reflexiona sobre sus procesos de pensamiento, se apoya en organizadores gráficos (por ejemplo, tablas o mapas mentales) para representarlos y evalúa su efectividad.
5) Posee auto-conocimiento y regula sus emociones, Asume responsabilidad sobre su bienestar y el de los otros, y lo expresa al cuidar su cuerpo, su mente y las relaciones con los demás
6) Tiene iniciativa y favorece la colaboración, Reconoce, respeta y aprecia la diversidad de capacidades y visiones al trabajar de manera colaborativa. Tiene iniciativa, emprende y se esfuerza por lograr proyectos personales y colectivos.
7) Asume su identidad, favorece la interculturalidad y respeta la legalidad, Se identifica como mexicano. Reconoce la diversidad individual, social, cultural, étnica y lingüística del país, y tiene conciencia del papel de México en el mundo.
8) Aprecia el arte y la cultura, Experimenta, analiza y aprecia distintas manifestaciones artísticas. Identifica y ejerce sus derechos culturales.
9) Cuida su cuerpo y evita conductas de riesgo, Activa sus destrezas motrices y las adapta a distintas situaciones que se afrontan en el juego y el deporte escolar
10) Muestra responsabilidad por el ambiente, Promueve el cuidado del medio ambiente de forma activa
11) Emplea sus habilidades digitales de manera pertinente, Compara y elige los recursos tecnológicos a su alcance y los aprovecha con una multiplicidad de fines.
Propósitos generales
1. Concebir las matemáticas como una construcción social en donde se formulan y argumentan hechos y procedimientos matemáticos.
2. Adquirir actitudes positivas y críticas hacia las matemáticas: desarrollar confianza en sus propias capacidades y perseverancia al enfrentarse a problemas; disposición para el trabajo colaborativo y autónomo; curiosidad e interés por emprender procesos de búsqueda en la resolución de problemas.
3. Desarrollar habilidades que les permitan plantear y resolver problemas usando herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
Propósitos para la educación primaria
1. Utilizar de manera flexible la estimación, el cálculo mental y el cálculo escrito en las operaciones con números naturales, fraccionarios y decimales.
2. Identificar y simbolizar conjuntos de cantidades que varían proporcionalmente, y saber calcular valores faltantes y porcentajes en diversos contextos.
3. Usar e interpretar representaciones para la orientación en el espacio, para ubicar lugares y para comunicar trayectos.
4. Conocer y usar las propiedades básicas de triángulos, cuadriláteros, polígonos regulares, círculos y prismas.
5. Calcular y estimar el perímetro y el área de triángulos y cuadriláteros, y estimar e interpretar medidas expresadas con distintos tipos de unidad.
6. Buscar, organizar, analizar e interpretar datos con un propósito específico, y luego comunicar la información que resulte de este proceso.
7. Reconocer experimentos aleatorios y desarrollar una idea intuitiva de espacio maestral.
B) ¿Cuál es el campo de formación que define las matemáticas en la educación básica?
Número, álgebra y variación
Numero
Adicción y sustracción
Multiplicación y división
Proporcionalidad
Ecuaciones
Funciones
Patrones, figuras geométricas y expresiones equivalentes
Forma, espacio y medida
Ubicación espacial
Figuras y cuerpos geométricos
Magnitudes y medidas
Análisis de datos
Estadística
Probabilidad
C) ¿Cuál es el perfil de egreso al término de cada nivel educativo de acuerdo en al ámbito de pensamiento matemático?
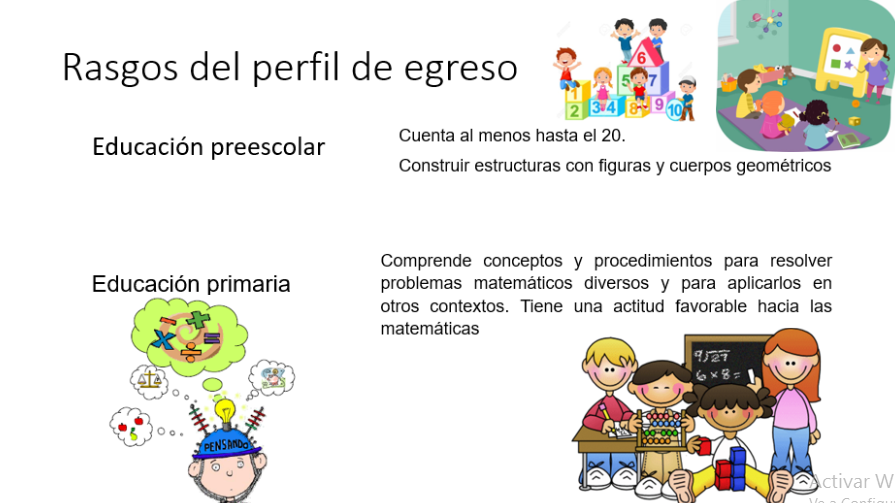
Al término de la educación preescolar
Cuenta al menos hasta el 20. Razona para solucionar problemas de cantidad, construir estructuras con figuras y cuerpos geométricos, y organizar información de formas sencillas (por ejemplo, en tablas).
Al término de educación primaria
Comprende conceptos y procedimientos para resolver problemas matemáticos diversos y para aplicarlos en otros contextos. Tiene una actitud favorable hacia las matemáticas
Al término de educación secundaria
Amplía su conocimiento de técnicas y conocimientos matemáticos para ampliar y resolver problemas con distinto grado de complejidad,así como para modelar y analizar situaciones. Valora las cualidades del pensamiento matemático
Al término de la educación media superior
Construye e interpreta situaciones reales, hipotéticas o formales que requieren la utilización del pensamiento matemático. Formula y resuelve problemas, aplicando diferentes enfoques.
3. Enfoque

4. Orientaciones didácticas

5. Preguntas de orientaciones didácticas
¿En qué consisten las orientaciones didácticas?
Aprender matemáticas es importante para aprender las siguientes metas:
comprender la situación implicada en un problema. Representa que los alumnos comprendan a fondo el problema e identifiquen la información esencial para resolverlo. Es conveniente averiguar como analizar la información que deben de manera oral o escrita.
Los alumnos proponen el camino a seguir. Tienen la posibilidad de: compartir ideas, abra acuerdos y desacuerdos, se expresaran con libertad y podrán reflexionar. El papel del docente es propiciar un diálogo productivo y no ofrecer soluciones .
Trabaja en equipo. Esta estrategia afecte a los alumnos la posibilidad de expresar sus ideas y enriquecerlos con las opciones de los demás, desarrollar una actitud de colaboración y la habilidad para fundamentar sus argumentos. El maestro debe insistir en que todos los integrantes asuman la responsabilidad de resolver la tarea, no de manera individual si no de colectiva.
Manejo adecuado del tiempo. Los alumnos resuelven problemas con sus propios medios, discuten y analizan sus procedimientos y sus resultados implican más tiempo. Si ellos comprenden lo que estudian, alcanzarán mejores resultados. Es indispensable prender tiempo para analizar lo que producen aclarar ideas, aportar información, explicación necesarias, tiempo para formar conocimiento en los problemas.
Diversificar el tipo de problema. Es favorable es la planificación actitudes adicionales para aquellos alumnos que puedan enfrentar situaciones más complejas o para los que necesiten apoyo para comprender los conceptos matemáticos.
Compartir experiencias con otros profesores. Será de gran ayuda que los maestros compartan experiencias entre ellas entorno al estudio de las matemáticas, pues sean estás exitosas o no, les permitirán mejorar permanentemente su trabajo.
6. Sugerencias de evaluación

7. Preguntas de sugerencias de evaluación
¿Cuál es el sustento teórico de las sugerencias de evaluación?
Tiene un enfoque formativo porque se centra en los procesos de aprendizaje y da seguimiento al progreso de los alumnos. Los errores de los alumnos son una oportunidad de aprendizaje para ellos y también para el maestro, en la medida en que estos se analicen, discutan y se tomen como base para orientar estrategias de aprendizaje.
De resolver problemas con ayuda a solucionarlos autónoma-mente Trabajo de manera autónoma de principio a fin obteniendo resultados correctos.
De la justificación pragmática al uso de propiedades. Interacción entre alumnos, objeto de conocimiento y maestro, generando la explicación de procedimientos y resultados.
De los procedimientos informales a los procedimientos expertos. Los alumnos usan procedimientos informales, y es tarea del maestro que dichos procedimientos evolucionen hacia otros cada vez más eficaces.
8. Aprendizajes

9. PRESENTACIÓN










ANÁLISIS DE LA PRIMERA UNIDAD.
En esta primera unidad se aprendieron los aprendizajes esperados a nivel básico primaria y aprendizajes esperados por nivel educativo , así como el enfoque pedagógico que es a través de la resolución de problemas, las orientaciones didácticas nos permiten tener una idea al maestro sobre como analizan la información los alumnos, así como trabajo en equipo. las sugerencias de evaluación nos permiten ver algunos aspectos que se pueden considerar para una evaluación formativa.
UNIDAD DE APRENDIZAJE II



Estrategias de enseñanza y aprendizaje para el desarrollo del concepto de número
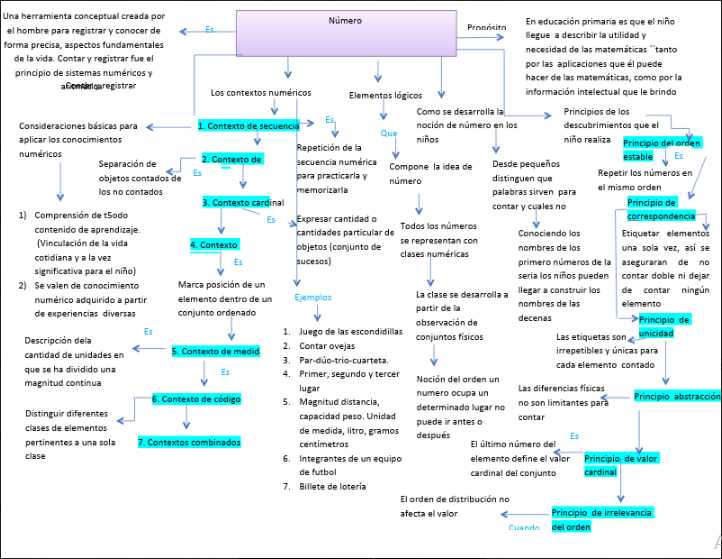
Número: es una herramienta conceptual creada por el hombre para registrar y conocer de forma precisa, aspectos fundamental de la vida. Contar y registrar fue el principio de la evolución de sistemas numéricos y aritméticos.
Propósito de la educación primaria respecto de la enseñanza de las matemáticas es que el niño llegue a describir la utilidad y necesidad de esta materia ´´tanto por las aplicaciones que él puede hacer de las matemáticas, como por la formación intelectual que le brinda´´. (sep, 1980 p.21).
Como logra el maestro que apliquen los conocimientos numéricos para resolver problemas de la vida cotidiana. Consideraciones básicas para aplicar los Conocimientos numéricos.
1. Comprensión de todo contenido de aprendizaje.
2. Vinculación de la vida cotidiana y a la vez significativa para el niño.
3. Conocimiento numérico adquirido a partir de experiencias cotidianas.
NÚMERO NATURAL (enteros positivos)
0-1-2-3-4-5-6-7-8-9
LOS CONTEXTOS NUMÉRICOS
1. Contexto de secuencia. Repetición de secuencia numérica para practicarla y memorizarla.( juego de las escondidas)
2. Contexto de conteo. Cada número pronunciado guarda una relación de correspondencia biunívoca con un objeto determinado.( separación de objetos contados de los no contados).
3. contexto cardinal. Expresar cantidades o una cantidad particular de objetos o sucesos. ( par, terna dúo, trió, cuarteto).
4. Contexto ordinal. Marcar posición de un elemento dentro de un conjunto ordenado.( primer lugar, segundo lugar).
5. Contexto de medida. Descripción de cantidad de unidades en que se a dividido una magnitud.( distancia, capacidad, peso, unidades de medida, litro, gramos o centímetros).
6. Contexto de código. Distinguir diferentes clases de elementos como etiquetas o símbolos, elementos que pertenecen a una sola clase. ( integrantes de un equipo de fútbol).
7.Contextos combinados( billete de lotería, número de serie, código de identificación).
Elementos lógicos que componen la idea de número.
Todos los números representan ´´clases numéricas´´ cuando evocamos un número lo que hacemos es identificar a que clase de número pertenece, la clase del uno, del dos, tres, cuatro (acción mental).
Los niños desarrollan la noción de clase numérica a partir de la observación de conjuntos físicos. Noción del número, desorden a orden, un número ocupada determinada posición en la serie de acuerdo con su magnitud.
La clasificación permite al niño entender las relaciones de clases numéricas. La clasificación por lo tanto, define la cardinalidad del número, mientras que la seriación su ordinalidad.
¿Cómo se desarrolla la noción de número en los niños?
Desde pequeños distingue las palabras que sirven para contar y cuales no.
Los nombres de los números se componen con las palabras que designa a las decenas y a las unidades. Conociendo los nombres de los primeros números de la serie, los niños pueden llegar a construir los nombres de las decenas.
PRINCIPIOS DE DESCUBRIMIENTO QUE EL NIÑO REALIZA.
1.Principio de orden estable.Los niños se dan cuenta de que contar requiere de repetir los números siempre con el mismo orden.
2. Principio de correspondencia. Para enumerar un conjunto es necesario etiquetar sus elementos una sola vez, de esta manera los niños se aseguran de no contar dos veces el mismo elemento, ni dejar de contar ninguno,
3. Principio de unicidad. Las etiquetas deben ser irrepetibles y únicas para cada elemento contado.
4. Principio de abstracción. Los niños descubren que las diferencias físicas no son una limitante para poder contar.
5. Principio de valor cardinal. A través de repetidas experiencias de conteo, los niños llegan a descubrir que el ultimo número pronunciado designa el valor cardinal del conjunto.
6. Principio de irrelevancia del orden. Al contar de varias maneras los elementos de un conjunto los niños pueden darse cuenta de que el orden o distribución no afecta el valor cardinal del conjunto.
Evolución curricular.
- El enfoque didáctico permanece,
- la actividad fundamental de la asignatura sigue siendo el razonamiento.
- El enfoque de la evaluación es formativo.
- Se retrasa el estudio de los ángulos.
- se omitieron múltiplos y submúltiplos del metro cuadrado.
- El estudio de la probabilidad se estudia ahora en primaria.
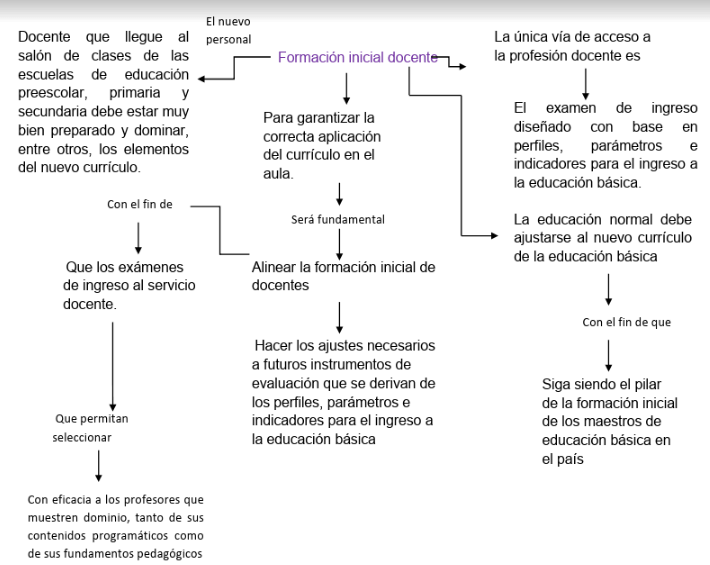
Formación inicial docente
El nuevo personal docente que llegue al salón de clases de las escuelas en educación preescolar, primaria y secundaria debe estar muy bien preparado y dominar, entre otros, los elementos del nuevo currículo.
La educación normal debe ajustarse al nuevo currículo de la educación básica, con el fin de que siga siendo el pilar de la formación inicial de los maestros de educación básica en el país.
La forma de enseñanza tiene que ir de lo concreto a lo abstracto. Tenemos que enseñar el concepto de número con distintos objetos visuales para que los niños empiecen a contar y así se familiarice con los números,
- concreto ( lo que manipula).
- gráfico( lo que dibuja)
- representación o icónica( representaciones figuradas)
- Numeral simbólico( símbolo o grupo de símbolos que representan a un número.
La descomposición es un proceso importante. No son monolíticos, se enseña a partir del número 3 la descomposición.
Conteo. Es una acción matemática que los niños necesitan practicar, el propósito es lograr que el proceso de contar se sintetice y se convierta en una herramienta que les ayude a resolver los primeros problemas matemáticos que se les presenten. El proceso de medir, denomina que los niños cuenten de manera convencional, o bien que hayan construido pautas estables al contar.
Orden. Es una cualidad intrinsica de los números naturales, aspecto que los alumnos deben aprender.
Números cardinales y ordinales; concretos y abstractos.
Se representan como números cardinales como uno, dos, tres, cuatro, cinco, seis, siete, ocho, nueve, y diez. Entonces se representan en los números ordinales como primero, segundo, tercero, cuarto, quinto, sexto, séptimo, octavo, noveno y décimo.
Sobre conteo, a partir de un número empezar a contar.
evidencias segunda unidad
Evolución curricular
Aspectos del currículo anterior que permanecen
1. Enfoque didáctico resolución de problemas
2. Problemas de interés
3. El aprendizaje se sustenta de las ideas previas de los alumnos para ir adquiriendo y complementándolas para la construcción de conocimientos complejos y el uso de técnicas eficaces.
4. La actividad fundamental de la asignatura es el razonamiento, complementando con la memoria y la práctica y así facilitar los procesos más complejos.
5. El enfoque de la evaluación es formativa, mejorando el desempeño de los alumnos, así como dar la
oportunidad de reflexionar sobre lo que saben, lo que están aprendiendo y lo que aprenderán
Hacia donde se avanza este currículo.
1. Se tiene una posición más clara sobre la concepción de las matemáticas y del papel de la resolución de problemas.
2. Las orientaciones didácticas se recuperan con explicaciones y sugerencias de actividades
3. Se integro el eje ¨ número álgebra y variación¨ que incluye proporcionalidad
4. En aritmética se nombran los temas de acuerdo con las operaciones básicas, se mantiene el estudio de sistema de numeración maya y romano
5. Se elimino el estudio de las proporcionalidad múltiple y el interés compuesto
6. Se retraso el estudio de los ángulos
7. Se omitieron múltiplos y submúltiplos del metro cuadrado
8. El estudio de la probabilidad se estudia ahora en primaria
ACTIVIDAD ORDEN DE LOS NÚMEROS.
¿QUÉ VENTAJAS DIDÁCTICAS PRESENTA EL HECHO DE QUE LOS ALUMNOS CONOZCAN
APROPIADAMENTE EL ORDEN DE LOS NÚMEROS NATURALES?
Que el alumno conozca, aplique y respete el orden de la secuencia de los números naturales con
diferentes estrategias didácticas para aplicarlas en distintos contextos.
Dentro de la aplicación de estrategias didácticas introducir el número cero para que en niño
entienda su valor.
¿ QUÉ VENTAJAS DIDÁCTICAS OFRECE EL HECHO OFRECE EL HECHO DE EMPLEAR COLECCIONES DE
OBJETOS EN ACTIVIDADES DONDE LOS ALUMNOS TIENEN QUE COMPARAR CANTIDADES?
Para identificar los principios de conteo que el niño maneja, como pueden ser: de orden,
correspondencia, cardinalidad y unicidad aplicadas en diferentes conjuntos de elementos.
Con el uso de diferentes estrategias didácticas se puede razonar entre las comparaciones que se
lleguen a realizar.
¿ QUÉ VENTAJAS DIDÁCTICAS OFRECE EL HECHO DE QUE LOS ALUMNOS SEPAN QUE UNA
COLECCIÓN PUEDE COMPONERSE O DESCOMPONERSE DE DISTINTAS MANERAS PARA
COMPRENDER LA RELACIÓN DE ORDEN EN LOS NÚMEROS NATURALES?
Para comprender y tener antecedentes de la suma y la testa.
Para que el niño a partir de un número determinado empiece a contar.
ANÁLISIS DE LA SEGUNDA UNIDAD.
En esta unidad se analizaron algunos aspectos sobre el concepto de número, así como algunas estrategias para que se puedan emplear con los alumnos al momento de ingresar este concepto, también se tomaron en cuenta el tipo de contexto de número; contexto de conteo, ordinal, código, y combinados, así mismo se abordo el tema de principios de descubrimiento que el niño realiza al momento de trabajar con los números como son; principio de orden estable, correspondencia, unicidad, abstracción, , de valor cardinal y el de irrelevancia del orden.
Es importante estar actualizado en tanto al nuevo modelo educativo, respecto a esto se tomo en cuenta la evolución curricular y se puede observar que el enfoque no a cambiado, pero si hay aspectos que cambian como que se retrasa el estudio de los ángulos.
UNIDAD DE APRENDIZAJE III




Estrategias de enseñanza y aprendizaje para el desarrollo del sentido numérico: suma y resta.
Característica de la suma. conmutativa, el orden de los sumandos no afecta el resultado.
La secuencia, se forma cuando se agrega una unidad al número anterior.
El conjunto, son coleccionados de casos y cada uno de ellos es un elemento del conjunto.En el conjunto de los números naturales para todo número natural N en el que le siga es N +1 y se llama el SUCESOR, de N, y de N se dice que es el ANTECESOR de N+1.
Las colecciones discretas, se presentan agrupados de alguna forma con esto se induce la idea de que una colección puede agruparse de diferentes maneras, lo cual se confirma usando materiales manipulables.
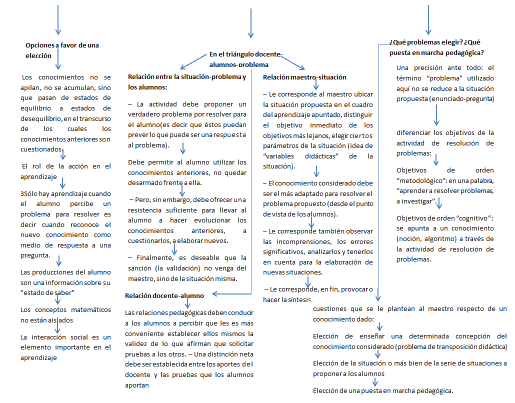
Teoría de situaciones didácticas
Situación didáctica
Planeación de la clase con la intención de que los alumnos aprendan reglas del minuendo.
variables, distintas respuestas a la resta.
Situación de acción, el alumno entra en contacto con el problema.
Situación de formulación, cunado el profesor da la indicación de que el alumno ya puede resolver el problema, es todo el proceso que realizan los estudiantes para poder llegar a una respuesta.
Situación de validación, se explica como fue que se llego a esa respuesta de forma grupal.
Institucionalización, se formaliza el conocimiento.
Situación a-didáctica.
Descubrimiento autónomo de las reglas.
Conocimiento, conocimientos previos para la resolución de la resta.
Sanción, cuando el niño se da cuenta de su error y lo corrige.
No intervención, los niños guían el trabajo por si solos.
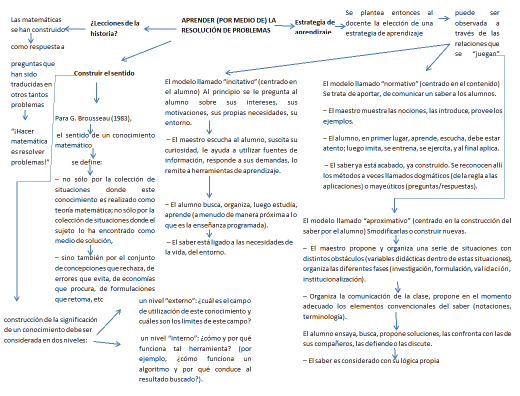
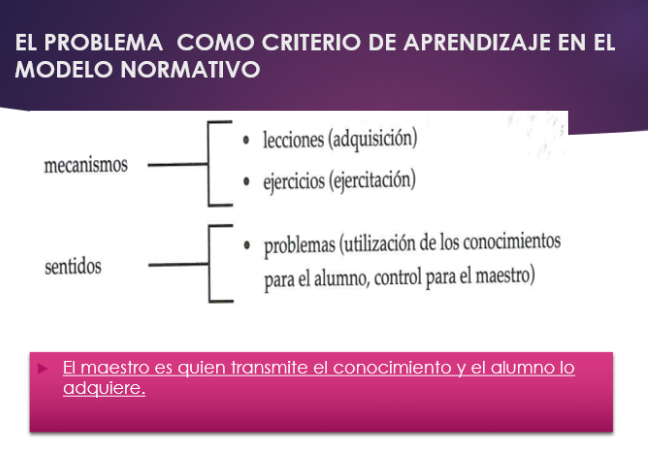
APRENDER (POR MEDIO DE) LA RESOLUCIÓN DE PROBLEMAS
Para G. Brousseau (1983),
el sentido de un conocimiento matemático se define: – no sólo por la colección de situaciones donde este conocimiento es realizado como teoría matemática; no sólo por la colección de situaciones donde el sujeto lo ha encontrado como medio de solución, – sino también por el conjunto de concepciones que rechaza, de errores que evita, de economías que procura, de formulaciones que retoma, etc
Estrategia de aprendizaje
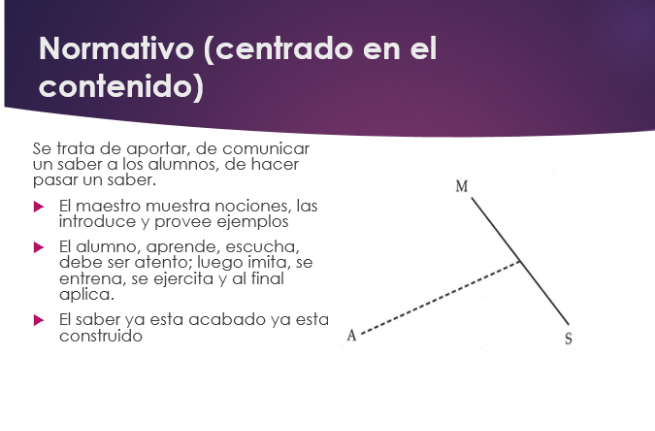
El modelo llamado “normativo” (centrado en el contenido) Se trata de aportar, de comunicar un saber a los alumnos. – El maestro muestra las nociones, las introduce, provee los ejemplos. – El alumno, en primer lugar, aprende, escucha, debe estar atento; luego imita, se entrena, se ejercita, y al final aplica. – El saber ya está acabado, ya construido. Se reconocen allí los métodos a veces llamados dogmáticos (de la regla a las aplicaciones) o mayeúticos (preguntas/respuestas).
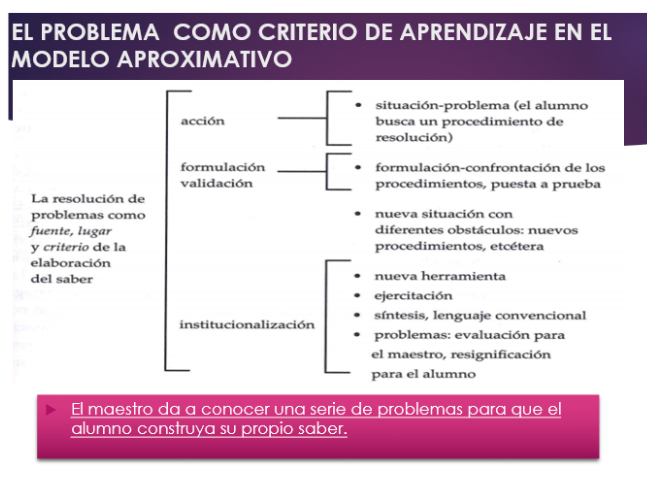
El modelo llamado “aproximativo” (centrado en la construcción del saber por el alumno) es modificarlas o construir nuevas. – El maestro propone y organiza una serie de situaciones con distintos obstáculos (variables didácticas dentro de estas situaciones), organiza las diferentes fases (investigación, formulación, validación, institucionalización). – Organiza la comunicación de la clase, propone en el momento adecuado los elementos convencionales del saber (notaciones, terminología). El alumno ensaya, busca, propone soluciones, las confronta con las de sus compañeros, las defiende o las discute. – El saber es considerado con su lógica propia.
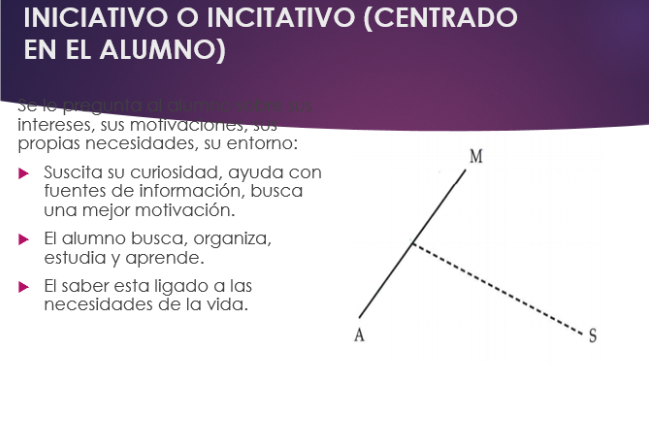
El modelo llamado “incitativo” (centrado en el alumno) Al principio se le pregunta al alumno sobre sus intereses, sus motivaciones, sus propias necesidades, su entorno. – El maestro escucha al alumno, suscita su curiosidad, le ayuda a utilizar fuentes de información, responde a sus demandas, lo remite a herramientas de aprendizaje. – El alumno busca, organiza, luego estudia, aprende (a menudo de manera próxima a lo que es la enseñanza programada). – El saber está ligado a las necesidades de la vida, del entorno.
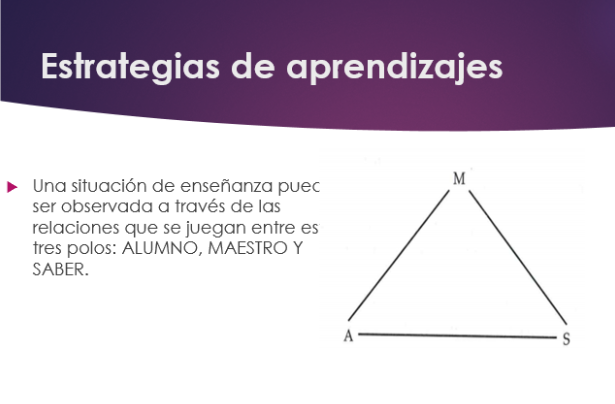
En el triángulo docente-alumnos-problema
Relación entre la situación-problema y los alumnos: – La actividad debe proponer un verdadero problema por resolver para el alumno(es decir que éstos puedan prever lo que puede ser una respuesta al problema). Debe permitir al alumno utilizar los conocimientos anteriores, no quedar desarmado frente a ella. – Pero, sin embargo, debe ofrecer una resistencia suficiente para llevar al alumno a hacer evolucionar los conocimientos anteriores, a cuestionarlos, a elaborar nuevos. – Finalmente, es deseable que la sanción (la validación) no venga del maestro, sino de la situación misma.
Relación docente-alumno Las relaciones pedagógicas deben conducir a los alumnos a percibir que les es más conveniente establecer ellos mismos la validez de lo que afirman que solicitar pruebas a los otros. – Una distinción neta debe ser establecida entre los aportes del docente y las pruebas que los alumnos aportan.
Relación maestro-situación – Le corresponde al maestro ubicar la situación propuesta en el cuadro del aprendizaje apuntado, distinguir el objetivo inmediato de los objetivos más lejanos, elegir ciertos parámetros de la situación (idea de “variables didácticas” de la situación). – El conocimiento considerado debe ser el más adaptado para resolver el problema propuesto (desde el punto de vista de los alumnos). – Le corresponde también observar las incomprensiones, los errores significativos., analizarlos y tenerlos en cuenta para la elaboración de nuevas situaciones. – Le corresponde, en fin, provocar o hacer la síntesis.
Los agrupamientos sucesivos les pueden ayudar a los niños a contar más rápido cuando la cantidad es muy grande.
PRINCIPIOS DEL SISTEMA DE NUMERACIÓN DECIMAL.
Principio de base; para avanzar en el conocimiento de la serie numérica de nuestro sistema de numeración decimal, es conveniente que los alumnos se enfrenten a situaciones que le permitan comprender la necesidad y las ventajas de agrupar los objetos de una colección en decenas, en un primer momento, y mas adelante en centenas, decenas, y en millares.
Principio de posición; El uso de la tabla o del ábaco para representar la cardinalidad de colecciones constituye un importante paso intermedio para llegar a la representación convencional de cantidades. El registrar cantidades en tablas favorece que los alumnos comprendan que cada cifra representa un agrupamiento distinto, según la posición que ocupa, es decir, que cada cifra contiene un valor relativo.
TIPOS DE PROBLEMAS VERBALES ADITIVOS SIMPLES-
La operación de adición asume dos significados. añadir, juntar o combinar elementos.
Acciones o relaciones semánticas, que caracterizan los cuatro tipos de problemas aditivos simples: CAMBIO, se da cuando una distribución produce un cambio o transformación en el conjunto inicial. COMBINACIÓN, se da cuando ninguno de los dos conjuntos se modifica. COMPARACIÓN, relación comparativa. IGUALACIÓN, es quitar o poner para llegar a una misma cantidad.
Tipo de relación; DINÁMICAS, CAMBIO E IGUALACIÓN.
ESTÁTICAS. COMBINACIÓN Y COMPARACIÓN.
Conocer las operaciones de suma y de resta va más aya de saber resolver cuentas de suma y de resta. Significa reconocer las situaciones en los que estás operaciones son útiles, saber escoger atinadamente un procedimiento para resolver una suma o resta dependiendo de las cantidades involucradas, poder dar resultados aproximados y saber aplicar ciertas propiedades de la suma y de la resta para facilitar los cálculos.
evidencias tercera unidad
1. Actividad orden-conteo
Dos procedimientos fundamentales asociados al número: agregar y completar, que son antecedentes no formales para las operaciones de suma y resta.
El objeto de consideración o no en la clase, plantean la percepción de totales y partes que los forman, sugieren que los números no son monolíticos, que se pueden descomponer en muchas formas. Estas percepciones son necesarias para la construcción de la noción de número y que el número conlleva en sí mismo las operaciones aritméticas
En el conjunto de los números naturales para todo número natural N el que le sigue es N+1 y se llama el sucesor de N. Y de N se dice que es el antecesor de N+1.
El conjunto o los conjuntos son colecciones de cosas y cada una de ellas es un elemento del conjunto. Contar una colección de objetos es algo más que establecer una correspondencia uno a uno entre una secuencia inicial de los números naturales y los elementos de la colección
a) De acuerdo con la información que presenta la guía enuncie las lecturas que puede darle a la Fig. 1.
Los pajaritos se ubican en un espacio formado por dos conjuntos de cinco troncos iguales uniformemente espaciados, en total diez troncos. Al “leer” las ilustraciones de arriba hacia abajo se observa la secuencia 1, 2, 3, 4 y 5. Mediante las imágenes se pide a los alumnos que registren sus respuestas en los cuadros en blanco.
Pero también pueden mirar invirtiendo el recorrido (5, 4, 3, 2 y 1) para completar los troncos vacíos y notar, de abajo hacia arriba, que faltan 5, 6, 7, 8 y 9 pajaritos. En cada imagen de troncos y pajaritos hay
Troncos con y sin pajaritos (sugiere 5=5+0;
4=4+0, etc.) Unos troncos chicos y otros grandes
• Hay manzanas, pero una es roja y otra verde
(Sugiere 2=1+1).
• Hay cinco pelotas, tres rosas y dos verdes
(Sugiere 5=3+2). Cuatro dentro del canasto y una fuera
• Hay cuatro lápices, tres rojos y uno azul
(Sugiere 4=3+1).dos chicos y dos grandes
b) ¿A qué nos inducen las imágenes como antecedentes no formales para las operaciones de suma y resta?
la noción de que los números se pueden componer y descomponer de distintas maneras a través de procedimientos que les son inherentes(esencial y permanente).
c) ¿Qué característica presenta la representación gráfica?
es que los conjuntos no son del todo homogéneos, presentan cualidades que permiten distinguir sus elementos
d) ¿En qué radica la importancia de la secuencia de los pajaritos?
radica en que introduce al niño en el “arte de contar”, de agregar y completar, que podemos construir un número a partir de otros. Esto permite introducir las nociones no formales de suma y resta sin necesidad de disponer de dos números, basta con uno que pueda descomponerse,
2. Actividades que se sugieren para los futuros docentes
1.¿Cuál es la intención didáctica de presentar los 10 troncos de la ilustración en esta página distribuidos en dos grupos de 5 troncos?
Ver que el niño pueda comprar los elementos de los conjuntos así como clasificar los tamaños de cada tronco.
Ver en que posición se encuentra cada pajarito
2.¿Cuáles son las ventajas didácticas que ofrece el hecho de usar colecciones no homogéneas en esta lección?
Realizar comparaciones entre las distintas características (principio de abstracción) de los objetos o imágenes.
Tener en cuenta las distintas formas en las que se puede impartir el tema de orden y conteo.
3. ¿Cuáles serían las limitaciones didácticas si sólo se emplearan colecciones homogéneas?
No se podría hacer comparaciones entre los distintos elementos y conjuntos ya que serían iguales.
Algunos niños no comprenderían como comprar.
3.CONCEPTOS DE LA TSD.
¿Cuáles son las dos posiciones epistemológicas de las que parte la didáctica de las matemáticas de la escuela francesa?
La identificación de la interpretación de fenómenos y procesos, objeto de interés supone el desarrollo de un cuerpo teórico, y no puede realizarse a observaciones a partir de experiencias. La convicción de que ese cuerpo teórico debe ser específico del saber matemático y no puede provenir de la simple aplicación de la teoría.
¿Cómo se concibe el aprendizaje en la teoría de situaciones didácticas?
Concepción constructivista. El alumno aprende adaptándose a un medio; este saber fruto de la adaptación alumno se manifiesta por las respuestas nuevas que son la prueba del aprendizaje.
¿Cuál es la diferencia entre una situación didáctica y una a-didáctica?
La primera es un conjunto de relaciones entre el alumno, un medio y un sistema educativo (maestro). En la segunda los conocimientos se ponen en práctica y se sanciona las decisiones que toma el alumno.
¿Cuáles son y en que consisten los aspectos que definen a una situación a-
didáctica?
La necesidad al conocimiento a que se apunta, es necesario para resolución de ciertos problemas. Sanción, el alumno interactúa con un medio que le ofrezca información sobre su producción (que el alumno juzgue sus resultados). No intervención, los alumnos deben encontrar por si mismos relaciones entre sus elecciones y resultados que obtienen.
¿Cuál es la intervención del maestro en una situación a-didáctica?
El alumno acepta la responsabilidad de una situación de aprendizaje.
¿Qué es una variable didáctica y como puede ser utilizada?
Son sujeto teórico cuya finalidad es estudiar el conjunto de condiciones y relaciones propias del conocimiento bien determinado. Puede utilizar valores que permitan al alumno comprender y resolver la situación con sus conocimientos previos, y luego hacerle afrontar la construcción de un conocimiento fijando un nuevo valor de una variable.
¿En qué consiste la institucionalización?
Define las relaciones que pueden tener los comportamientos o producciones ¨libres¨ del alumno con el saber cultural o científico y con el proyecto didáctico.
4.Mapa conceptos básicos.

5. VÍDEO 1
a) Explique su propia idea de lo que podrían hacer los niños para solucionar la situación planteada.
El alumno podría dividir y multiplicar
b) ¿Cómo inicia la clase el maestro, y en general que rol juega en los distintos momentos de la clase.?
Plantea el problema tomando en cuenta que todos los alumnos lo entiendan (situación de acción, el alumno entra en contacto con el problema) Resolución del problema El rol que juega es importante ya que deja que los alumnos manejen un enfoque constructivista, el sólo es una guía para los alumnos, realiza cuestiones para hacer comprobaciones, criterio de no intervención los alumnos deben encontrar por si mismos relaciones entre sus elecciones y resultados
c) La importancia que representa el momento de la confrontación de resultados (para maestro y alumnos)
El maestro verificó las diferentes variables posibles para el resultado con anterioridad.En esta etapa se lleva a cabo es aspecto didáctico de institucionalización ya que el maestro hace una reflexión y comparación entre las diferentes formas de llevar al resultado. La sanción, el alumno ve la información que le ofrece sus resultados ( el alumno juzga sus resultados)
d) Las acciones que realiza el maestro ante los errores que cometen los alumnos.
Deja que con la ayuda de sus compañeros los que tienen errores se den cuenta por si solos con el fin de no evidenciar a ninguno.Conoce los resultados que obtuvieron los alumnos.Ve los distintos procedimientos para llegar al resultado Validación: los alumnos están de acuerdo que hay diferentes procedimientos para llegar al resultado, explicación de lo aprendido.
6.VÍDEO 2
a) Identifica la manera en que el profesor presenta el problema y explica su intención y el propósito de la actividad de enseñanza, los aprendizajes que espera que logren los alumnos.
Clase experimental: El profesor presenta unos cuadros de papel en la cual por la parte de atrás tiene el número, el único número que se ve es el resultado de la resta. La intención del maestro es que los alumnos tienen que averiguar la ecuación de la resta que conduzca al resultado (tres). Los estudiantes encontraran ciertas reglas ocultas en las respuestas de los problemas.
1: que el minuendo y es sustraendo se incrementan el uno.
2: hay los mismos números de ecuaciones como el valor de la diferencia
Si lo estuantes conocen las reglas pueden encontrar las diferentes maneras pueden encontrar todas las maneras posibles de minuendos y sustraendos más rápidamente
b) El profesor empezó la clase donde la diferencia es 3, ¿así lo planeó originalmente?, Explica por qué empezó con este caso.
Sí, porque así los alumnos lograrían darse cuenta del orden de las operaciones y las posibles formas de realizar las operaciones
c) Al inicio del video algunos niños se expresaron acerca del profesor ¿por qué los alumnos quieren a su profesor? ¿Puede explicar su respuesta a partir de la forma en que él prepara la clase?
Les gusta en muchas formas, es lindo, es buena persona, Si por que sus clases de matemáticas son divertidas e interesantes
d) En el video, un niño dijo: “Señor Seiyama, hay algo mal en las respuestas”. ¿Por qué dijo ese niño “hay algo mal en las respuestas” y muchos de sus compañeros estaban de acuerdo con él?
Se dio cuenta que había algo mal en las respuestas, no estaban en orden. Porque la mayoría se dio cuenta ya que el orden de las ecuaciones debería ser reacomodado
e) Aunado a estas respuestas relacione lo acontecido en el vídeo con la Teoría de Situaciones Didácticas. Planeación de la clase con la intención de que los alumnos aprendan las reglas del minuendo y sustraendo en esas restas.
Variables, distintas respuestas a la resta. Situación de acción: el alumno entra en contracto con el problema. Formulación: cuando el profesor la información par que el alumno pueda resolver el problema y cuando los alumnos participan para comparar resultados. Validación: explicación de lo aprendido Institucionalización: el profesor complementa y retroalimenta lo aprendido, formalizando los términos. Situación a didáctica: descubrimiento autónomo de las reglas. Necesidad de conocimiento: conocimientos previos para la realización de la resta Sanción, cuando el niño se dio cuenta del orden y lo corrige, cuando se da cuenta que el minuendo y el sustraendo va en orden.No intervención, los niños descubrieron por si solos.
7. Mapa aprender por medio de la resolución de problemas.
8. Presentación aprender por medio de la resolución de problemas.




9.TRIPTICO


10. PRÁCTICA GUÍA DE OBSERVACIÓN
Algunos de los aspectos que conviene que observen son los siguientes:
¿Cómo organizó el maestro al grupo para que realizaran la actividad?
Algunas actividades se realizaron de forma individual, otra en parejas y una de forma grupal.
¿En qué consistió la actividad planteada por el maestro?
La primera que fue individual los alumnos realizaron cálculo mental.
La segunda se realizó de forma individual fueron unas sumas con unidades y decenas.
La tercera fue grupal se les entregó la mitad de una hoja milimétrica y recortaron rectángulos con 10
cuadros dentro, después pasar algunos cuadros para formar decenas y ver cuanto era.
¿Cómo se usó el libro de texto gratuito?
Las sumas y la actividad de decenas y centenas venían en el libro de texto y de ahí tomo los ejemplos para poder impartir la clase.
¿Cuál fue la consigna (indicaciones) dada por el maestro?
Sacar la libreta para el cálculo mental, colocar la fecha del día de hoy, y colocar un listado de números del 1 al 5 como está en el pizarrón. La actividad de sumas ya estaba empezada cuando llegue así que no escuche indicaciones( primer día) Lupita, Ailyn repartan los libros de matemáticas, Diego, Luis repartan las libretas la maestra Rebe pasará a calificar la tarea y el cálculo mental mientras hacemos la actividad, coloquen la fecha mientras la maestra, Rebe reparte una hoja que se va a ocupar.
¿Cuál fue la actitud de los alumnos frente a la actividad?
Ellos estaban tranquilos y felices
¿Cuáles procedimientos o recursos fueron utilizados por los niños para realizar la
actividad?
Sumar con los dedos, hacían operaciones, colocaban palitos en la libreta, contaban los cuadritos, pedían ayuda a la maestra.
¿Qué hizo el maestro mientras los alumnos realizaban la actividad?
Les ayudaba si tenían dudas, calificar otras actividades, estaba en el teléfono, veía que todos los alumnos estuvieran trabajando.
¿Cuál fue la actitud del maestro frente a las participaciones y respuestas de los
alumnos?
La muestra estaba feliz de que la mayoría de los alumnos participarán en los ejercicios y a la hora de ver los errores.
¿Cómo se validaron los procedimientos y respuestas de los alumnos?
La muestra paso a algunos alumnos que querían participar para dar respuesta la actividad y si estaban mal no se los decía como tal sino que pedía que le ayudarán los compañeros.
¿Qué contenidos matemáticos se trabajaron al realizar la actividad y a qué eje temático
corresponden?
Número, álgebra y variación.
Número, adición y sustracción.
¿Qué aprendieron los alumnos al realizar la actividad?
11.Conclusión de la práctica.
De acuerdo con la teoría de situaciones didácticas pudimos rescatar las siguientes
teorías y aspectos en las escuelas.Teoría didáctica: cuando el maestro planificó su clase tomando en cuenta los conocimientos previos de los alumnos para construir nuevos, con distintos materias didácticos (bate lenguas, colores, hojas y tarjetas). Dentro de esta teoría identificamos las siguientes situaciones: Acción, cuando el maestro da por primera ves el problema y los alumnos entran en contacto con el, enfrentamiento a la resolución del problema. Formulación, los maestros interactúan con los alumnos así como alumnos con alumnos. Validación, cuando comparten sus respuestas con todo el grupo tomando en cuenta los diferentes procedimientos por los cuales se puede llegar al resultado(variables). No intervención, el maestro hace que los alumnos se mantienen concentrados en el problema y cuando se distraen hace que vuelvan a el.
Yo creo que en la mayoría de los salones en las dos escuelas se toma en cuenta la teoría de situaciones didácticas ya que es el sustento para llevar a cabo el enfoque, sin embargo consideró que deberían utilizar más la devolución para que los alumnos puedan resolver los problemas solos, ya que por lo observado el maestro ayudaba bastante a los alumnos dándolo las respuestas o la forma en como se tiene que hacer.
12. Vídeo de la clase de matemáticas primer año.
De acuerdo con el vídeo puede observar algunos aspectos como los siguientes
Teoría didáctica, el maestro utilizó una caja y dentro de ella tenía 30 tapas para
que los alumnos comprendieran el problema.
El maestro dio instrucciones y luego dio el problema así sucede la situación de acción ya que los alumnos entran en contacto con el problema cuando él maestro lea dice que encuentren cuantas tapan quedan en la caja después de que un compañero saco 10 tapas y así empieza la resolución del problema. Devolución, los alumnos realizan el problema solos aceptado la responsabilidad de resolverlo. La no intervención, el maestro hace que los alumnos que están trabajando en equipo estén concentrados en el problema. Los alumnos encuentran varias formas de resolver el problema (variables previstas por el profesor) utilizando representaciones irónicas Formulación, el maestro interactúa con los alumnos preguntando cosas sencillas Y los alumnos interactúan entre ellos para ver como lo van a resolver y si están de acuerdo con el resultado Validación, cuando del maestro pregunta si están de acuerdo de que el resultado es 20 y todos dicen que si. Institucionalización, el maestro completa y retroalimenta lo aprendido sacando y contando las tapas que quedaron dentro de la caja confirmando el resultado de todos.
Yo creo que el maestro si utiliza algunos aspectos de la teoría de situaciones didácticas ya que es fundamental para el enfoque porque las matemáticas están en la vida diaria en procesos sencillos como ir a comparar. Hacer operaciones pequeñas con la mente. Aprender a sumar cantidades menores y mayores de 100 Comprendieron mejor el como se completa una decena. Su opinión general sobre el desarrollo de la clase, el papel del maestro y de los alumnos. Yo creo por lo que puede observar los tres días que el desarrollo de la clase se fue dañado conforme los alumnos iban comprendiendo lo que estaban realizando, en mi opinión la maestra es buena y paciente con los alumnos para que puedan comprender lo que hacen, los alumnos participan con gran entusiasmo sólo que se distraen con gran facilidad y eso hace que se desvíe un poco la clase sin embargo la profesora trata de que todos estén atentos en la clase.
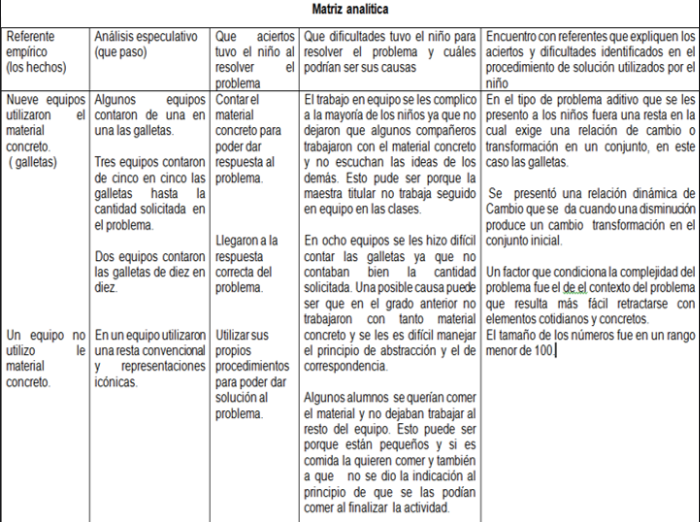
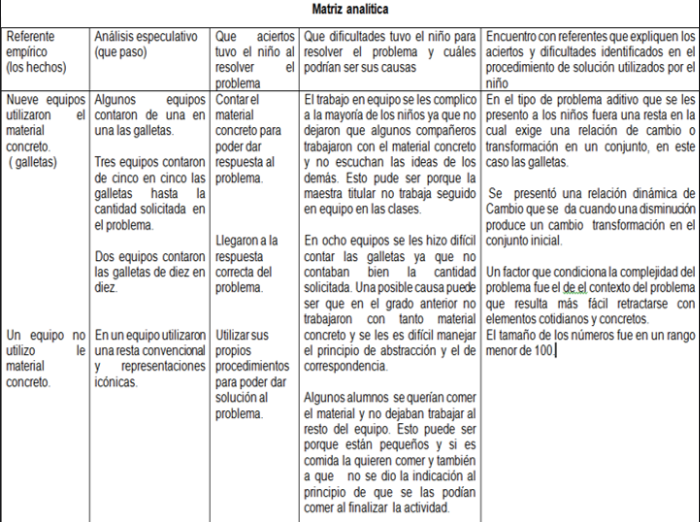
13. Matriz analítica.
14. Presentación proceso de aprendizaje del niño respecto a la suma y resta














ANÁLISIS DE LA TERCERA UNIDAD.
Al momento de querer introducir la suma y la resta no se tiene que empezar con un algoritmo, si no que se tiene que introducir a través de la resolución de problemas, esto permite que los niños estén más interesados pro resolver el problema. Al momento de empezar a resolver problemas de suma y resta es importante que los alumnos lo empiecen a realizar a través de material concreto.
La teoría de situaciones didácticas es el sustento para el enfoque pedagógico. Al momento de realizar una secuencia didáctica o planeación se tiene que tomar en cuenta aspectos dicha teoría como son: situación de acción, situación de formulación y situación de validación. El modelo que se tiene que utilizar dentro de un aula es el modelo aproximativo que esta centrado en la construcción del saber por el alumno.
Hay diferentes tipos de problemas aditivos simples que se pueden utilizar para que el alumno trabaje, estos son; cambio, combinación, comparación e igualación. Dentro de estos hay dos tipos de de relación; dinámica y estática.
UNIDAD DE APRENDIZAJE IV




Estrategias de enseñanza y aprendizaje para el desarrollo del sentido numérico: multiplicación y división.
La multiplicación y la división.
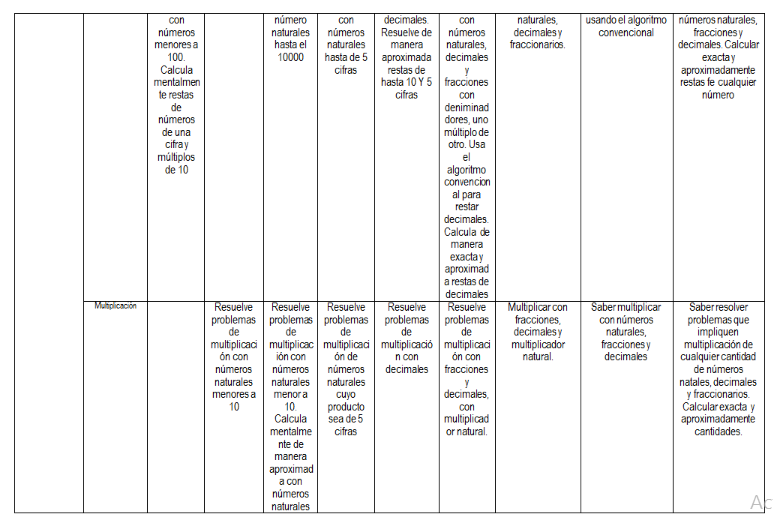
La enseñanza de la multiplicación y la división no es únicamente que los alumnos sepan ejecutar los algoritmos correspondientes, se pretende que los niños logren una comprensión amplia del sentido de estas operaciones que pueden aplicarlas para para resolver una variedad de problemas y que dispongan de estrategias adecuadas entre las cuales están las técnicas usuales.
- niños logren una comprensión amplia del sentido de estas operaciones.
- Que puedan aplicarlas con flexibilidad para resolver una variedad de problemas cada vez mayor
- Que sean capaces de proporcionar mentalmente resultados aproximados, dispongan estrategias de cálculo
LA MULTIPLICACIÓN: es una suma iterada porque se repite.
Cuando se aborda un problema nuevo con frecuencia es necesario desarrollar recursos informales, procesos de ensayo y error, antes de encontrar una manera sistemática de resolverlo
Por ejemplo “el diagrama de árbol´”. Ayuda a organizar el total de combinaciones posibles y encontrar las operaciones que permiten calcular ese total .
El uso de la multiplicación representa un paso fundamental en el proceso de aprender a dividir.
Dos tipos de problemas de multiplicación.
En la multiplicación con números naturales se pueden identificar los siguientes tipos de problemas
•uno es aquel que establece una relación proporcional entre dos medidas
• y otro aquellos en los que se multiplican las medidas de dos magnitudes para obtener la medida de una tercera magnitud.
Los problemas de multiplicación mas familiares para los niños y mas adecuados para introducir esta operación son en los que se establece una relación proporcional entre las medidas de dos magnitudes.
Actividades y juegos con la multiplicación
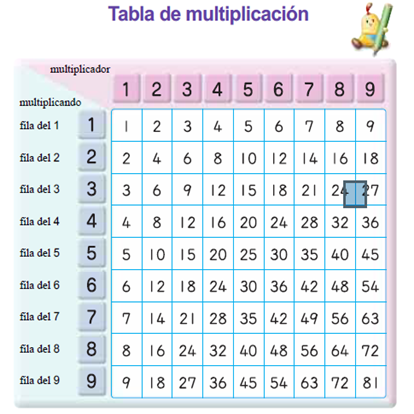
Es una actividad que se puede aplicar para que los estudiantes observen y analicen:
❑La posibilidad de intercambiar al multiplicando y al multiplicador sin alterar el producto.
5x6 = 6x5
❑Cuáles renglones tienen múltiplos en común.
❑Que en el primer renglón y en la primera columna, el multiplicador o el multiplicando, según sea el caso se repiten justo cuando su valor es 1 (el neutro multiplicativo).
Los alumnos tienen la oportunidad de buscar estos y más secretos en la tabla de multiplicar o pitagórica.
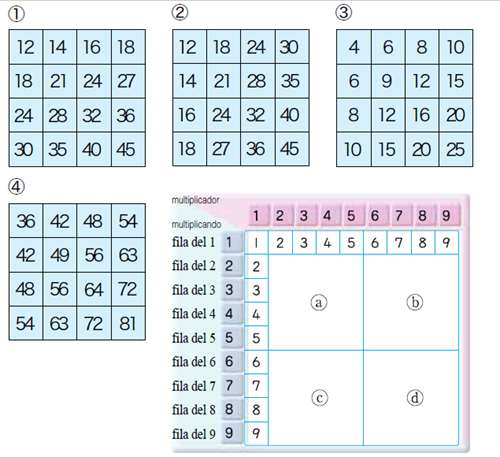
Esta actividad consiste en reconstruir la tabla de multiplicar a partir de cuatro cuadrados de dimisiones iguales. Implica
❑Que los estudiantes tengan una idea de cómo aumentan los resultados en la tabla.
❑Es importante que el niño conozca “el incremento” y que este sea progresivo.
Con base a estas actividades o juegos los estudiantes van construyendo las tablas de multiplicar y no las aprenden de memoria.
❑se propicia que se memoricen las tablas con la realización de muchos ejercicios.
PROPIEDADES DE LA MULTIPLICACIÓN.
Propiedad conmutativa: en la multiplicación el resultado es el mismo si el multiplicando y el multiplicador intercambian su posición.
Ejemplo:
7x5=35 5x7=35
Propiedad distributiva: se descompone uno de los factores en sumandos, de esta manera se aplica de forma implícita la propiedad.
Ejemplo:
3x12=36
(3x6)+ (3x6)
18+18=36
Elemento neutro 1
Ejemplo:
1x1=1
1x2=2
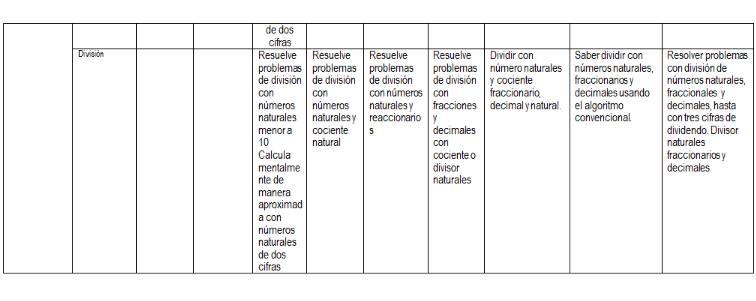
DIVISIÓN.
Cuando los alumnos enfrentan problemas de división en tercer y cuarto grado normalmente ya tienen conocimiento sobre la suma la resta y la multiplicación esto les permite desarrollar una gran variedad de procedimientos para dividir antes de abordar el procedimiento usual.
División de reparto equitativo
Se usa para repartir cosas entre niños de modo que cada uno reciba la misma cantidad.
Cuando los alumnos llegan a resolver operaciones buscando el número que multiplicado de el producto es porque han empezado concebir de manera implícita a la división como multiplicación inversa.
Dos tipos de problemas de división
Agrupamiento o tasativa: se relaciona dos magnitudes del mismo tipo y se trata de ver cuántas veces cabe una en la otra.
De reparto: se relacionan magnitudes de distinto tipo y puede decirse que se trata de repartir una en la otra.
Los niños a través de la experiencia en la resolución de problemas van construyendo poco a poco las relaciones necesarias para saber que corresponden a determinada operación. No es necesario que aprendan a distinguir la estructura de los problemas ,ni mucho menos que se aprendan los nombres de estas estructuras.
División como sustracción iterada. Es una operación aritmética que permite encontrar cuántas veces un número está contenido en otro puede abordarse como operación inversa de la multiplicación.
División con resto.El residuo es un elemento importante de la división cuyo significado puede variar de acuerdo al contexto
División con uno y con cero.
•Se abordan los casos de la división con el mismo dividendo y divisor y con cero como dividendo en el transcurso de una situación similar de reparto equitativo en la que varía el dividendo a para Hallar el valor del cociente
•Cualquier número dividido entre sí mismo es uno
4 entre 4 = 1
•0 dividido entre un número diferente de cero es cero
0 entre 4 igual a cero.
PROPIEDAD DE LA DIVISIÓN.
Cundo el dividendo aumenta de tres en tres y el divisor es el mismo, el cociente aumenta de uno en uno, no cambia.
Cuando el dividendo aumenta de tres en tres y el divisor aumenta de uno en uno, el cociente es el mismo, relación cociente- dividendo.
EVIDENCIAS CUARTA UNIDAD
1. Calculo mental
1 ¿ cuáles son las características más importantes del cálculo mental ?
Calculo mental es una expresión que convoca ha pocas imágenes y suscita adhesiones, rechazos, dudas y expectativas. Hay dos tipos de cálculo el primero duele denominarse cálculo automático o mecánico , y se refiere a la utilización de un algoritmo o de un material (contador , regla de cálculo, calculadora, tabla de algoritmos, etcétera). El segundo es llamado cálculo reflexivo o reanudo.
Cálculo mental es el conjunto de procedimientos que, analizando los datos por tratar, se articulan, sin recurrir a un algoritmo preestablecido, para obtener resultados exactos o aproximados.
Los procedimientos de cálculo mental se apoyan en las propiedades del sistema de numeración decimal y en las operaciones, y poner en juego diferentes tipos de escritura de los números así como diversas relaciones entre los números.
El cálculo mental ese una vía de exceso para la comprensión y los construcción de algoritmos.
El trabajo sobre el cálculo mental tiene carácter articulador.
Los rapidez no es una característica ni in valor, aunque puede ser una herramienta en situaciones didácticas en los que, por ejemplo, les permita a los alumnos distinguir aquellos cálculos de los que dispongan los resultados en memoria de los que no
2 ¿ Qué ventajas ofrece en estudio de las matemáticas?
Responder a la demanda social plantea una aproximación al cálculo que haga a los alumnos capaces de elegir los procedimientos, encontrar resultados y juzgar validez de las respuestas.
Los aprendizajes en terreno del cálculo manera influyen en la capacidad de resolver problemas. El enriquecimiento de las relaciones numéricas a través del cálculo mental favorecen que los alumnos, ante una situación, sean capaces de modelizarla, por anticipación, por reflexión. Que los alumnos puedan establecer relaciones numéricas (pensar) y sacar conclusiones a partir de esas relaciones
El cálculo mental acrecienta el conocimiento en el campo numérico. Las actividades del cálculo mental propones el cálculo como objeto reflexión, favoreciendo la aparición y el tratamiento de relaciones estrictamente matemáticas.
El trabajo del cálculo mental habilita un modo de construcción del conocimiento que, a nuestro entender, favorece una mejor relación del alumno con la matemática. Que los alumnos puedan articular lo que saben con lo que tiene que aprender. Que los alumnos establezcan una relación más personal con el conocimiento, en aparición al frente sentimiento de ajenidad que la mayoría de las personas tiene con la matemática.
El trabajo de cálculo pensado debe ser acompañado por un acrecentamiento progresivo al cálculo automático. Liberar espacio mental. Memorización de cálculos simples.
3 ¿En qué situaciones de la vida diaria se utilizan las matemáticas?
De cotidianeidad, son muchas las situaciones vinculadas al cálculo mental:
La estimulación de los gastos de una compara de supermercado pata no exceder el dinero que se lleva
El cálculo de los ingredientes de una receta para el doble de personas.
La preparación de un presupuesto global de una fiesta o salida.
Redondeando cantidades y precios. Etcétera.
4 ¿ Qué actividades de cálculo mental se pueden utilizar en la escuela?
Utilizar ampliamente actividades grupales de aprendizaje que favorecen los intercambios, la discusión y la reflexión sobre las experiencias matemáticas.
La construcción paralelo y vinculación del cálculo pensado y del cálculo automático requieren que se lleve adelante, sistemáticas, dos tipos de actividades:
Un trabajo de memorización de repertorios y reglas, a medida que se han ido construyendo, y
Un trabajo colectivo, lento y detallado, de aprendizaje del cálculo mental pensado, que se apoya en la comparación de diversos procedimientos utilizados por distintos chicos para tratar el problema.
El maestro selecciona y propone cálculos que favorecen procedimientos reconstructivos.
En este sentido es importante analizar cuáles son los recursos y clases de actividades que se pueden proponer en función de los objetivos que se dediquen para casa clase o periodo de trabajo.
El juego tiene un rol importante, por un lado permiten que empiece a haber en la clase más trabajo independiente por parte de los alumnos, aprender a respetar reglas, a ejercer roles diferenciados, a distribuir, a llegar a acuerdos. Por otro lado brindan al docente mayores oportunidades de observar, e incluso trabajar más intensamente con quienes lo necesitan.
Cuando se trabajan repertorios (aditivos, sustractivos, multiplicación), se proponen actividades tendientes a que todos los alumnos los dominen.
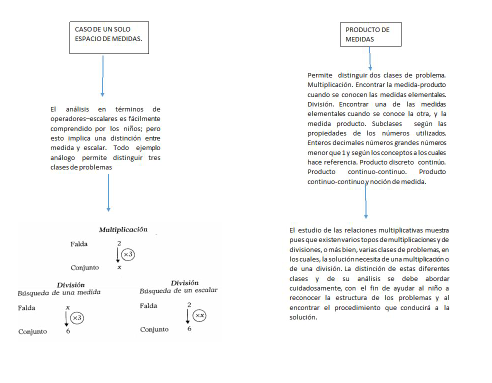
2. Mapa los problemas de tipo multiplicativo.


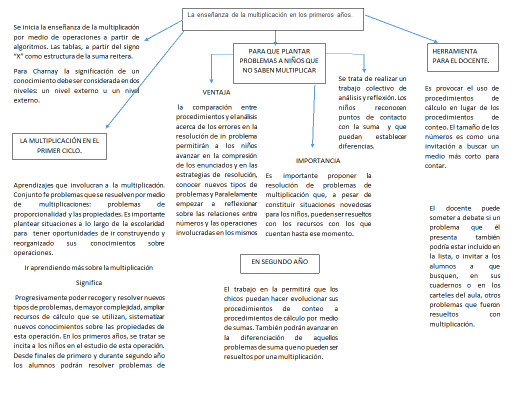
3. Mapa la enseñanza de la multiplicación en los primeros años.



4. Presentación multiplicación y división










5. DOCUMENTO EXPLICATIVO

“2018. Año del Bicentenario del Natalicio de Ignacio Ramírez Calzada. El Nigromante”
LICENCIATURA EN EDUCACIÓN PRIMARIA
Plan de estudios 2018
PRIMER GRADO PRIMER SEMESTRE
CURSO: Aritmética números naturales.
DOCUMENTO EXPLICATIVO MULTIPLICACIÓN Y DIVISIÓN
ESTUDIANTE: REBECA GONZÁLEZ GÁLVEZ
PROFA: VERÓNICA MORA ROJAS
CICLO ESCOLAR 2018 – 2019
TOLUCA, MÉXICO, ENERO DE 2019
La multiplicación y la división.
La enseñanza de la multiplicación y la división no es únicamente que los alumnos sepan ejecutar los algoritmos correspondientes, se pretende que los niños logren una comprensión amplía del sentido de estas operaciones que puedan aplicarlos para resolver una variedad de problemas y que dispongan de estrategias adecuadas entre los cuales están las técnicas usuales.
La multiplicación es una suma iterada (repetida), se puede introducir la noción de multiplicación a través de distintas actividades como se muestra en las siguientes imágenes.

El uso de la tabla pitagórica nos sirve para que el niño descubra algunos secretos que esta contiene como por ejemplo: la tabla es simétrica respecto a la diagonal, propiedad conmutativa, elemento neutro el uno.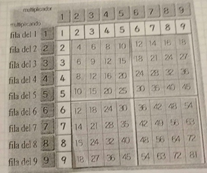
Entré los problemas de multiplicación con números naturales, pueden distinguirse dos tipos:
Aquellos en los que se establece una relación proporcional entre dos medidas y aquellas en los que se multiplican las medidas de dos magnitudes para obtener la medida de una tercera magnitud.
El uso de la multiplicación representa un paso importante en el proceso de aprender a dividir.
Propiedades de la multiplicación:
Propiedad conmutativa; en la multiplicación el resultado es el mismo si el multiplicando y el multiplicador intercambian su posición.
Ejemplo: 5x6=30 6x5=30
Propiedad distributiva; se descompone uno de los factores en sumandos, de esta manera se aplica de forma implícita esta propiedad.
Ejemplo:
- 3x12=36
(3x6) + (3x6)
18+18=36
Elemento neutro 1
Ejemplo 1x1=1 1×2=2 1x3=3
La división.
Cuando los alumnos enfrentan problemas de división en tercer y cuarto grado normalmente ya tienen conocimiento sobre la suma la resta y la multiplicación esto les permite desarrollar una gran variedad de procedimientos para dividir antes de abordar el procedimiento usual
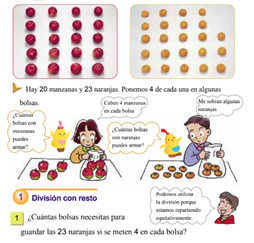
División de reparto equitativo.
Se usa para repartir cosas entre niños de modo que cada uno reciba la misma cantidad
Sugieren hallar la cantidad que recibe cada niño de manera que reparto del total de bloques sea equitativo.
Estos problemas de reparto son un antecedente para propiciar que los niños asignan un sentido y significado a la división.
En las primeras resoluciones de problemas de reparto los alumnos suelen utilizar el procedimiento de reparto cíclico (uno por uno).
Esta actividad conduce a que los niños usen la tabla de multiplicar del 3 y con ello determinar la cantidad de bloques para cada niño y hallar el producto más cercano a 15

DOS TOPOS DE PROBLEMAS DE DIVISIÓN.
- Agrupamiento o tasativa: se relaciona dos magnitudes del mismo tipo y se trata de ver cuántas veces cabe una en la otra
Ejemplo. Se tiene 220 dulces y se quieren poner 4 dulces en cada bolsa ¿Cuántas bolsas se necesitan?
Ana tiene 20 dulces y quiere dar cuatro a cada uno de sus amigos ¿A cuántos amigos les puede dar dulces?
De reparto: se relacionan magnitudes de distinto tipo y puede decirse que se trata de repartir una en la otra.
Por ejemplo:
- 720 naranjas se reparten en 12 costales
- 20 dulces se reparten entre 5 niños
Los problemas de reparto en contexto de dinero resultan útiles para introducir a los alumnos en el conocimiento y ejecución del algoritmo usual para dividir este tipo de problemas ayuda a comprender el significado de la cantidad que se van obteniendo cada vez que se realizan paso de la técnica
DIVISIÓN COMO SUSTRACCIÓN ITERADA O REPETIDA
- Es una operación aritmética que permite encontrar cuántas veces un número está contenido en otro puede abordarse como operación inversa de la multiplicación.
- La operación 12 entre 4 puede realizarse al sustraer de manera iterada 4 unidades de 12, el número de veces que la sustracción lo permita.
- Ejemplo:
12 - 4 = 8
8 - 4 = 4
4 - 4 = 0
DIVISIÓN CON RESTO
El residuo es un elemento importante de la división cuyo significado puede variar de acuerdo al contexto
La división con resto se conoce formalmente como división euclidiana y se enuncia así de la siguiente manera:
DIVISIÓN CON UNO Y CON CERO
- Se abordan los casos de la división con el mismo dividendo y divisor y con cero como dividendo en el transcurso de una situación similar de reparto equitativo en la que varía el dividendo a para Hallar el valor del cociente
- Cualquier número dividido entre sí mismo es uno
4 entre 4 = 1
- 0 dividido entre un número diferente de cero es cero
0 entre 4 igual a cero
La división como operación aritmética
Ejemplo: 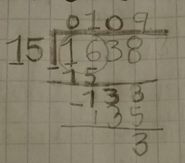
Propiedad de la división:
Cuando el dividendo aumenta de 3 en 3 y el divisor es el mismo, el cociente aumenta de uno en uno. No cambia
Ejemplo:
- 3÷3 =1
- 6÷3= 2
- 9x3=3
- 12x3=3
Cuando en dividendo aumenta de tres en tres y el divisor aumenta de uno en uno, el cociente es el mismo 3... Relación cociente – dividendo.
Ejemplo:
- 3÷1=3
- 6÷2=3
- 9÷3=3
- 12÷4=3.
De acuerdo con la lectura de Claudia Broitman (1998). La enseñanza de la multiplicación en los primeros años.
Para Charnay la significación de un conocimiento debe ser considerada en dos niveles: un nivel externo u un nivel externo.
La multiplicación en el primer ciclo. Aprendizajes que involucran a la multiplicación. Conjunto fe problemas que se resuelven por medio de multiplicaciones: problemas de proporcionalidad y las propiedades. Es importante plantear situaciones a lo largo de la escolaridad para tener oportunidades de ir construyendo y reorganizado sus conocimientos sobre operaciones.
Ir aprendiendo más sobre la multiplicación... Significa progresivamente poder recoger y resolver nuevos tipos de problemas, de mayor complejidad, ampliar recursos de cálculo que se utilizan, sistematizar nuevos conocimientos sobre las propiedades de esta operación. En los primeros años, se tratar se incita a los niños en el estudio de esta operación. Desde finales de primero y durante segundo año los alumnos podrán resolver problemas de partición por procedimientos de conteo, de reparto y por sumas sucesivas.
1. Qué pueden abordar la multiplicación en niños de primer segundo año. Aún cuando los niños no hayan aprendido “ la cuenta de multiplicar “ se trata de que empiecen a tener contacto con problemas “ diferentes “ desde su punto de vista y de que movilice nuevos recuerdo para resolverlos. Los niños no tienen una estrategia “experta “, Pero pueden generar una respuesta.
Ventaja,la comparación entre procedimientos y el análisis acerca de los errores en la resolución de in problema permitirán a los niños avanzar en la compresión de los enunciados y en las estrategias de resolución, conocer nuevos tipos de problemas y Paralelamente empezar a reflexionar sobre las relaciones entre números y las operaciones involucradas en los mismos.
2. Diferentes problemas de multiplicación en segundo y tercer año. Los problemas de multiplicación remiten a un mismo tipo de problemas: los de proporcionalidad, la mayoría de los problemas que los niños resuelven en la escuela y también la vida cotidiana pertenecer a esta categoría. Vergnaud propone también un análisis al campo de problemas multiplicativos, al que define como el conjunto de situaciones que se resuelven por medio de multiplicaciones o divisiones.
3: La utilización del signo “X”. Para los niños no es necesario conocer la utilización del signo X antes de la resolución de problemas. Si el signo no es incluido por algunos niños en los primeros problemas que resuelven la presentación del signo como producto de un a convención social del uso difundido y accesible hoy al mundo de los niños. Sr varía el tipo de desafío que se les propone a los alumnos unas vez realizadas las primeras actividades... Otra actividad que pretende provocar el uso del signo X es un mensaje corto para identifique el cálculo que han recibido. PROPIEDAD la propiedad conmutativa, el orden de los factores no afecta el producto. Para el abordaje de la escritura multiplicativa también pueden ponerse problemas de cuadriculados.
4. Por qué la memorización de resultados y las propiedades de la multiplicación. Hay que aprender las tablas porque es importante para que los niños Puedan resolver cuentas. Los niños necesitan progresivamente disponer de un conjunto de cálculos sencillos para realizar otros más complejos. .
5. La cuenta de multiplicar. A fines del primer año, los niños podrán resolver algunos sencillos problemas que involucran la multiplicación, utilizando dibujos y procedimientos de conteo, con la finalidad de que resuelvan actuaciones para las cuales no conocen directamente el cálculo. Durante segundo año estarán en condiciones de reconocer, frente a un problema, la cuenta de suma que permite resolverlo. Posteriormente se empezará a exigir a lis niños que escriban, luego de la suma reitera, cuál es el producto que sintetiza la operación.
De acuerdo a la lectura de Vergnaud, Tipos de problemas multiplicativos.
Se pueden distinguir dos grandes categorías de relaciones multiplicativas definimos así a las relaciones que comportan una multiplicación o una división. La mas importante de ellas, que se utiliza para la introducción de la multiplicación de la escuela primaria y que forma la trama de la gran mayoría de los problemas de topo multiplicativo, es una relación cuaternaria y no una relación ternaria.
ISOMORFISMO DE LAS MEDIDAS. La primera gran forma de la relación multiplicativa es una relación cuaternaria entre cuatro cantidades; dos cantidades son medidas de un cierto tipo, y el resto son medidas de otro tipo.
EJEMPLOS:
- Tengo 3 paquetes de yogur. Hay 4 yogur en cada paquete. ¿Cuántos yogures tengo?
- Mi mamá quiere comparar una tela que cuesta 24.80 francos el metro para hacerse un traje sastre. Necesita 3.50 metros de tela. ¿Cuánto deberá pagar?
- Compro 11 botellas de vino. Cada paquete de tres cuesta 19.50 francos. ¿Cuánto debo pagar?
Diferentes grados de dificultad que pueden ser representados por un esquema análogo, que no tiene ninguna dificultad pata los niños y que muestra muy claramente que son cuatro las cantidades puestas en relación. X designa la cantidad buscada.
Análisis dimensional el cuál permite dilucidar completamente las relaciones que intervienen en una multiplicación y mostrar así que la multiplicación más elemental hace intervenir de hecho un cálculo relacional referido a cuatro cantidades y varios topos de operaciones.
ANÁLISIS VERTICAL. Se centra en la noción de operador- escalar (sin dimensión) que hace pasar de una línea a otra en una misma categoría de medidas. La noción de fracción es introducida aquí a partir de la noción de dos operadores multiplicativos simples, una división y una multiplicación.

Se sabe que esta composición de operadores multiplicativos es, como la composición de transformación aditiva, una ley de grupo conmutativo (conmutatividad, elemento neutro, inverso). La conmutatividad permite invertir el orden de aplicación de los operadores elementales y efectuar.
El operador fraccionario representa pues de manera sintética la aplicación sucesiva de dos operadores multiplicativos (una división y una multiplicación) comenzando ya sea por la división o la multiplicación. Se puede considerar también que el operador fraccionario representa la multiplicación por la razón.
La noción de la razón, la razón – operador y la proporción son difíciles para los niños. Él maestro debe introducir estás nociones prudentemente, defendiéndose en cada etapa y apoyándose al máximo de las nociones más evidentes para el niño, como la de operador.
Análisis. 1 búsqueda de la solución del problema, pasando por la unidad y e valor unitario v.
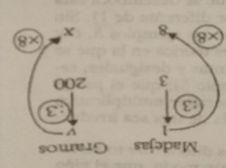
2 aplicación sucesiva de dos operadores (división primero).
3 estructura del operador fraccionario (simple convención de estructura en este nivel).
4 aplicación sucesiva de dos operadores (multiplicación primero, por conmutatividad).

5.Noción de razón, y de razón – operador.

6. proporción o igualdad de razones.

7. igualdades de razones- operadores.

8. regla de tres: análisis de estructura.

ANÁLISIS HORIZONTAL (función) está centrado en la noción F operador- función que hace pasar de una categoría a otra.
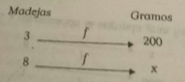
Si la noción de correspondencia no presenta ninguna dificultad ni su representación en forma de tabla el análisis de esa correspondencia en términos de función es por su parte mucho más delicado pues está implica no sólo la noción de relación numéricas sin igualmente la de consciente la de cociente de dimensiones producto de media medida esta forma de relación consiste en una relación ternaria entre 3 cantidades de las cuales eso es el producto de las otras dos tantos de plano numérico como en el plano dimensional.
Conclusión sobre la noción de dimensión
El análisis dimensional permite incluso establecer tal relación de una manera muy simple en efecto la utilización de un operador función para la solución de los problemas de la primera forma ISOMORFISMO de medidas permite encontrar la segunda forma producto de medida.
Clases de problemas de tipo multiplicativo pueden extraer se numerosos clases de problemas según la forma de relación multiplicativa el carácter discreto o continuo de las cantidades intervienen las propiedades de los números utilizados etcétera
Distinguir la las principales clases de problemas isomorfismo de medidas el cual pon en juego 4 cantidad espero los problemas más simples se sabe que una de estas es igual a 1 hay entonces grandes clases de problemas según incógnita sea alguna de las otras tres cantidades.
Multiplicación. División búsqueda del valor unitario. División búsqueda de la cantidad de unidades. Cada una de las clases se subdivide en numerosas subclases Multiplicación.

CASO DE UN SOLO ESPACIO DE MEDIDAS. El análisis en términos de operadores – escalares es fácilmente comprendido por los niños; pero esto implica una distinción entre medida y escalar. Todo ejemplo análogo permite distinguir tres clases de problemas

PRODUCTO DE MEDIDAS. Permite distinguir dos clases de problema. Multiplicación. Encontrar la medida-producto cuando se conocen las medidas elementales. División. Encontrar una de las medidas elementales cuando se conoce la otra, y la medida producto. Subclases según las propiedades de los números utilizados. Enteros decimales números grandes números menor que 1 y según los conceptos a los cuales hace referencia. Producto discreto continúo. Producto continuo -continuo. Producto continuo-continuo y noción de medida.
ANÁLISIS DE LA CUARTA UNIDAD.
Para que los niños aprendan la multiplicación y división tienen que reflexionar.
La multiplicación es una suma iterada. hay dos tipos de problemas los de una relación proporcional los cuales son mas adecuados para que los niños empiecen a trabajar sobre ellos. Y otro aquellos en los que se multiplican las medidas de dos magnitudes para obtener una tercera. Es importante que los alumnos encentren dos propiedades de la multiplicación; la conmutativa y la distributiva.
La división es un reparto.
Hay dos tipos de problemas de división; la tasativa o agrupamiento y de reparto, los cuales se pueden utilizar para que los niños empecen a trabajar con la división. También esta la división como sustracción iterada, con resto, con uno y con cero.
los alumnos deben de darse cuenta de las propiedades de la división; cuando el dividendo aumenta en la misma cantidad y el divisor es el mismo, el cociente aumenta de uno en uno. Cuando el dividendo aumenta en la misma cantidad y el divisor aumenta de uno en uno, el cociente es el mismo, relación cociente-dividendo.
