1. Calculo mental

1 ¿ cuáles son las características más importantes del cálculo mental ?

Calculo mental es una expresión que convoca ha pocas imágenes y suscita adhesiones, rechazos, dudas y expectativas. Hay dos tipos de cálculo el primero duele denominarse cálculo automático o mecánico , y se refiere a la utilización de un algoritmo o de un material (contador , regla de cálculo, calculadora, tabla de algoritmos, etcétera). El segundo es llamado cálculo reflexivo o reanudo.

Cálculo mental es el conjunto de procedimientos que, analizando los datos por tratar, se articulan, sin recurrir a un algoritmo preestablecido, para obtener resultados exactos o aproximados.

Los procedimientos de cálculo mental se apoyan en las propiedades del sistema de numeración decimal y en las operaciones, y poner en juego diferentes tipos de escritura de los números así como diversas relaciones entre los números.

El cálculo mental ese una vía de exceso para la comprensión y los construcción de algoritmos.

El trabajo sobre el cálculo mental tiene carácter articulador.

Los rapidez no es una característica ni in valor, aunque puede ser una herramienta en situaciones didácticas en los que, por ejemplo, les permita a los alumnos distinguir aquellos cálculos de los que dispongan los resultados en memoria de los que no

2 ¿ Qué ventajas ofrece en estudio de las matemáticas?

Responder a la demanda social plantea una aproximación al cálculo que haga a los alumnos capaces de elegir los procedimientos, encontrar resultados y juzgar validez de las respuestas.

Los aprendizajes en terreno del cálculo manera influyen en la capacidad de resolver problemas. El enriquecimiento de las relaciones numéricas a través del cálculo mental favorecen que los alumnos, ante una situación, sean capaces de modelizarla, por anticipación, por reflexión. Que los alumnos puedan establecer relaciones numéricas (pensar) y sacar conclusiones a partir de esas relaciones

El cálculo mental acrecienta el conocimiento en el campo numérico. Las actividades del cálculo mental propones el cálculo como objeto reflexión, favoreciendo la aparición y el tratamiento de relaciones estrictamente matemáticas.

El trabajo del cálculo mental habilita un modo de construcción del conocimiento que, a nuestro entender, favorece una mejor relación del alumno con la matemática. Que los alumnos puedan articular lo que saben con lo que tiene que aprender. Que los alumnos establezcan una relación más personal con el conocimiento, en aparición al frente sentimiento de ajenidad que la mayoría de las personas tiene con la matemática.

El trabajo de cálculo pensado debe ser acompañado por un acrecentamiento progresivo al cálculo automático. Liberar espacio mental. Memorización de cálculos simples.

3 ¿En qué situaciones de la vida diaria se utilizan las matemáticas?

De cotidianeidad, son muchas las situaciones vinculadas al cálculo mental:

La estimulación de los gastos de una compara de supermercado pata no exceder el dinero que se lleva

El cálculo de los ingredientes de una receta para el doble de personas.

La preparación de un presupuesto global de una fiesta o salida.

Redondeando cantidades y precios. Etcétera.

4 ¿ Qué actividades de cálculo mental se pueden utilizar en la escuela?

Utilizar ampliamente actividades grupales de aprendizaje que favorecen los intercambios, la discusión y la reflexión sobre las experiencias matemáticas.

La construcción paralelo y vinculación del cálculo pensado y del cálculo automático requieren que se lleve adelante, sistemáticas, dos tipos de actividades:

Un trabajo de memorización de repertorios y reglas, a medida que se han ido construyendo, y

Un trabajo colectivo, lento y detallado, de aprendizaje del cálculo mental pensado, que se apoya en la comparación de diversos procedimientos utilizados por distintos chicos para tratar el problema.

El maestro selecciona y propone cálculos que favorecen procedimientos reconstructivos.

En este sentido es importante analizar cuáles son los recursos y clases de actividades que se pueden proponer en función de los objetivos que se dediquen para casa clase o periodo de trabajo.

El juego tiene un rol importante, por un lado permiten que empiece a haber en la clase más trabajo independiente por parte de los alumnos, aprender a respetar reglas, a ejercer roles diferenciados, a distribuir, a llegar a acuerdos. Por otro lado brindan al docente mayores oportunidades de observar, e incluso trabajar más intensamente con quienes lo necesitan.

Cuando se trabajan repertorios (aditivos, sustractivos, multiplicación), se proponen actividades tendientes a que todos los alumnos los dominen.

2. Mapa los problemas de tipo multiplicativo.

3. Mapa la enseñanza de la multiplicación en los primeros años.

4.  Presentación multiplicación y división 

5. DOCUMENTO EXPLICATIVO 

“2018. Año del Bicentenario del Natalicio de Ignacio Ramírez Calzada. El Nigromante”

LICENCIATURA EN EDUCACIÓN PRIMARIA

Plan de estudios 2018

PRIMER GRADO               PRIMER SEMESTRE

CURSO: Aritmética números naturales.

DOCUMENTO EXPLICATIVO MULTIPLICACIÓN Y DIVISIÓN 

ESTUDIANTE: REBECA GONZÁLEZ GÁLVEZ 

PROFA: VERÓNICA MORA ROJAS 

CICLO ESCOLAR 2018 – 2019

TOLUCA, MÉXICO, ENERO DE 2019

La multiplicación y la división.

La enseñanza de la multiplicación y la división no es únicamente que los alumnos sepan ejecutar los algoritmos correspondientes, se pretende que los niños logren una comprensión amplía del sentido de estas operaciones que puedan aplicarlos para resolver una variedad de problemas y que dispongan de estrategias adecuadas entre los cuales están las técnicas usuales.

La multiplicación es una suma iterada (repetida), se puede introducir la noción de multiplicación a través de distintas actividades como se muestra en las siguientes imágenes.

El uso de la tabla pitagórica nos sirve para que el niño descubra algunos secretos que esta contiene como por ejemplo: la tabla es simétrica respecto a la diagonal, propiedad  conmutativa, elemento neutro el uno.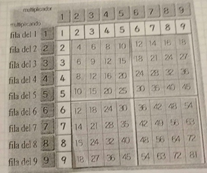

Entré los problemas de multiplicación con números naturales, pueden distinguirse dos tipos:

Aquellos en los que se establece una relación proporcional entre dos medidas y aquellas en los que se multiplican las medidas de dos magnitudes para obtener la medida de una tercera magnitud.

El uso de la multiplicación representa un paso importante  en el proceso de aprender a dividir.

Propiedades de la multiplicación:

Propiedad conmutativa; en la multiplicación el resultado es el mismo si el multiplicando y el multiplicador intercambian su posición.

Ejemplo: 5x6=30     6x5=30

Propiedad distributiva; se descompone uno de los factores en sumandos, de esta manera se aplica de forma implícita esta propiedad.

Ejemplo:

• 3x12=36

          (3x6) + (3x6)

           18+18=36

Elemento neutro 1

Ejemplo  1x1=1      1×2=2     1x3=3

La división.

Cuando los alumnos enfrentan problemas de división en tercer y cuarto grado normalmente ya tienen conocimiento sobre la suma la resta y la multiplicación esto les permite desarrollar una gran variedad de procedimientos para dividir antes de abordar el procedimiento usual

División de reparto equitativo.

Se usa para repartir cosas entre niños de modo que cada uno reciba la misma cantidad

Sugieren hallar la cantidad que recibe cada niño de manera que reparto del total de bloques sea equitativo.

Estos problemas de reparto son un antecedente para propiciar que los niños asignan un sentido y significado a la división.

En las primeras resoluciones de problemas de reparto los alumnos suelen utilizar el procedimiento de reparto cíclico (uno por uno).

Esta actividad conduce a que los niños usen la tabla de multiplicar del 3 y con ello determinar la cantidad de bloques para cada niño y hallar el producto más cercano a 15

DOS TOPOS DE PROBLEMAS DE DIVISIÓN.

• Agrupamiento o tasativa: se relaciona dos magnitudes del mismo tipo y se trata de ver cuántas veces cabe una en la otra

Ejemplo. Se tiene 220 dulces y se quieren poner 4 dulces en cada bolsa  ¿Cuántas bolsas se necesitan?

Ana tiene 20 dulces y quiere dar cuatro a cada uno de sus amigos ¿A cuántos amigos les puede dar dulces?

De reparto: se relacionan magnitudes de distinto tipo y puede decirse que se trata de repartir una en la otra.

Por ejemplo:

• 720 naranjas se reparten en 12 costales
• 20 dulces se reparten entre 5 niños      

Los problemas de reparto en contexto de dinero resultan útiles para introducir a los alumnos en el conocimiento y ejecución del algoritmo usual para dividir este tipo de problemas ayuda a comprender el significado de la cantidad que se van obteniendo cada vez que se realizan paso de la técnica

DIVISIÓN COMO SUSTRACCIÓN ITERADA O REPETIDA 

• Es una operación aritmética que permite encontrar cuántas veces un número está contenido en otro puede abordarse como operación  inversa de la multiplicación.
• La operación 12 entre 4 puede realizarse al sustraer de manera iterada 4 unidades de 12, el número de veces que la sustracción lo permita.
• 
  
•  Ejemplo:

12 - 4 = 8

8 - 4 = 4

4 - 4 = 0

DIVISIÓN CON RESTO

El residuo es un elemento importante de la división cuyo significado puede variar de acuerdo al contexto

La división con resto se conoce formalmente como división euclidiana y se enuncia así de la siguiente manera:

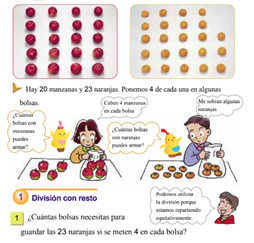
DIVISIÓN CON UNO Y CON CERO

• Se abordan los casos de la división con el mismo dividendo y divisor y con cero como dividendo en el transcurso de una situación similar de reparto equitativo en la que varía el dividendo a para Hallar el valor del cociente
• Cualquier número dividido entre sí mismo es uno

                                        4 entre 4 = 1

• 0 dividido entre un número diferente de cero es cero

                                    0 entre 4 igual a cero

La división como operación aritmética   

Ejemplo: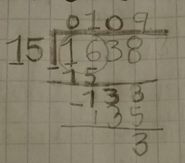  

Propiedad de la división: 

Cuando el dividendo aumenta de 3 en 3  y el divisor es el mismo, el cociente aumenta de uno en uno. No cambia

Ejemplo:

• 3÷3 =1
• 6÷3= 2
• 9x3=3
• 12x3=3

Cuando  en dividendo aumenta de tres en tres y el divisor aumenta de uno en uno, el cociente  es el mismo 3... Relación cociente – dividendo.

Ejemplo:

• 3÷1=3
• 6÷2=3
• 9÷3=3
• 12÷4=3.

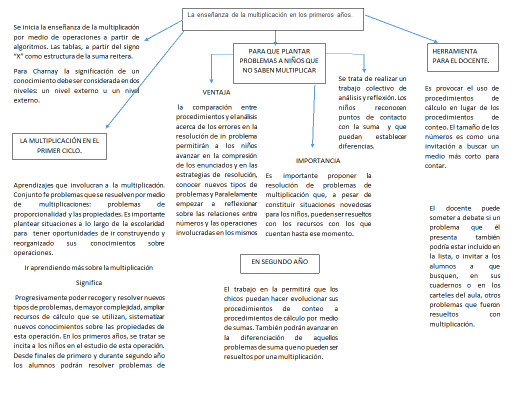
 De acuerdo con la lectura de Claudia Broitman (1998). La enseñanza de la multiplicación en los primeros años.

Para Charnay la significación de un conocimiento debe ser considerada en dos niveles: un nivel externo u un nivel externo.

La multiplicación en el primer ciclo. Aprendizajes que involucran a la multiplicación. Conjunto fe problemas que se resuelven por medio de multiplicaciones: problemas de proporcionalidad  y las propiedades. Es importante plantear situaciones a lo largo de la escolaridad para  tener oportunidades de ir construyendo y reorganizado sus conocimientos sobre operaciones.

Ir aprendiendo más sobre la multiplicación... Significa progresivamente poder recoger y resolver nuevos tipos de problemas, de mayor complejidad, ampliar recursos de cálculo que se utilizan, sistematizar nuevos conocimientos sobre las propiedades de esta operación. En los primeros años, se tratar se incita a los niños en el estudio de esta operación. Desde finales de primero y durante segundo año los alumnos podrán resolver problemas de partición por procedimientos de conteo, de reparto y por sumas sucesivas.

1. Qué pueden abordar la multiplicación en niños de primer segundo año.  Aún cuando los niños no hayan aprendido “ la cuenta de multiplicar “ se trata de que empiecen a tener contacto con problemas “ diferentes “ desde su punto de vista y de que movilice nuevos recuerdo para resolverlos. Los niños no tienen una estrategia “experta “, Pero pueden generar una respuesta.

Ventaja,la comparación entre procedimientos y el análisis acerca de los errores en la resolución de in problema permitirán a los niños avanzar en la compresión de los enunciados y en las estrategias de resolución, conocer nuevos tipos de problemas y Paralelamente empezar a reflexionar sobre las relaciones entre números y las operaciones involucradas en los mismos.

2. Diferentes problemas de multiplicación en segundo y tercer año. Los problemas de multiplicación remiten a un mismo tipo de problemas: los de proporcionalidad, la mayoría de los problemas que los niños resuelven en la escuela y también la vida cotidiana pertenecer a esta categoría. Vergnaud propone también un análisis al campo de problemas multiplicativos, al que define como el conjunto de situaciones que se resuelven por medio de multiplicaciones o divisiones.

3: La utilización del signo “X”. Para los niños no es necesario  conocer la utilización del signo X antes de la resolución de problemas. Si el signo no es incluido por algunos niños en los primeros problemas que resuelven la presentación del signo como producto de un a convención social del uso difundido y accesible hoy al mundo de los niños. Sr varía el tipo de desafío que se les propone a los alumnos unas vez realizadas las primeras actividades... Otra actividad que pretende provocar el uso del signo X es un mensaje corto para identifique el cálculo que han recibido. PROPIEDAD la propiedad conmutativa, el orden de los factores no afecta el producto. Para el abordaje de la escritura multiplicativa también pueden ponerse problemas de cuadriculados.

4.  Por qué  la memorización de resultados y las propiedades de la multiplicación. Hay que aprender las tablas porque es importante para que los niños Puedan resolver cuentas. Los niños necesitan progresivamente disponer de un conjunto de cálculos sencillos para realizar otros más complejos. .

5. La cuenta de multiplicar. A fines del primer año, los niños podrán resolver algunos sencillos problemas que involucran la multiplicación, utilizando dibujos y procedimientos de conteo, con la finalidad de que  resuelvan actuaciones para las cuales no conocen directamente el cálculo. Durante segundo año estarán en condiciones de reconocer, frente a un problema, la cuenta de suma que permite  resolverlo. Posteriormente se empezará a exigir a lis niños que escriban, luego de la suma reitera, cuál es el producto que sintetiza la operación.

De acuerdo a la lectura de Vergnaud,  Tipos de problemas multiplicativos.

Se pueden distinguir dos grandes categorías de relaciones multiplicativas definimos así a las relaciones que comportan una multiplicación o una división. La mas importante de ellas, que  se utiliza para la introducción de la multiplicación de la escuela primaria y que forma la trama de la gran mayoría de los problemas de topo multiplicativo, es una relación cuaternaria y no una relación ternaria.

ISOMORFISMO DE LAS MEDIDAS. La primera gran forma de la relación multiplicativa es una relación cuaternaria entre cuatro cantidades; dos cantidades son medidas de un cierto tipo, y el resto son medidas de otro tipo.

EJEMPLOS:

• Tengo 3 paquetes de yogur. Hay 4 yogur en cada paquete. ¿Cuántos yogures tengo?
• Mi mamá quiere comparar una tela que cuesta 24.80 francos el metro para hacerse un traje sastre. Necesita 3.50 metros de tela. ¿Cuánto deberá pagar?
• Compro 11 botellas de vino. Cada paquete de tres cuesta 19.50 francos. ¿Cuánto debo pagar?

 Diferentes grados de dificultad que pueden ser representados por un esquema análogo, que no tiene ninguna dificultad pata los niños y que muestra muy claramente que son cuatro las cantidades puestas en relación. X designa la cantidad buscada.

Análisis dimensional el cuál permite dilucidar completamente las relaciones que intervienen en una multiplicación y mostrar así  que la multiplicación más elemental hace intervenir de hecho un cálculo relacional referido a cuatro cantidades y varios topos de operaciones.

ANÁLISIS VERTICAL. Se centra en la noción de operador- escalar  (sin dimensión) que hace pasar de una línea a otra en una misma categoría de medidas. La noción de fracción es introducida aquí a partir de la noción de dos operadores multiplicativos simples, una división y una multiplicación.

 Se sabe que esta composición de operadores multiplicativos es, como la composición de transformación aditiva, una ley de grupo conmutativo (conmutatividad, elemento neutro, inverso). La conmutatividad permite invertir el orden de aplicación de los operadores elementales y efectuar.

El operador fraccionario representa pues de manera sintética la aplicación sucesiva de dos operadores multiplicativos (una división y una multiplicación) comenzando ya sea por la división o la multiplicación. Se puede considerar también que el operador fraccionario representa la multiplicación por la razón. 

La noción de la razón, la razón – operador  y la proporción son difíciles para los niños. Él maestro debe introducir estás nociones prudentemente, defendiéndose en cada etapa y apoyándose al máximo de las nociones más evidentes para el niño, como la de operador.

Análisis. 1 búsqueda de la solución del problema, pasando por la unidad y e valor unitario v.

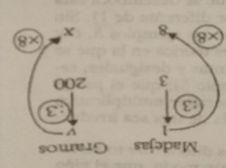
2 aplicación sucesiva de dos operadores (división primero).

3 estructura del operador fraccionario (simple convención de estructura en este nivel).

4 aplicación sucesiva de dos operadores (multiplicación primero, por conmutatividad).

5.Noción de razón, y de razón – operador.

 6. proporción o igualdad de razones.

7. igualdades de razones- operadores.

8. regla de tres: análisis de estructura.

ANÁLISIS HORIZONTAL  (función)  está centrado en la noción  F operador- función  que hace pasar de una categoría a otra.

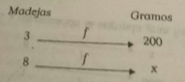
Si la noción de correspondencia no presenta ninguna dificultad ni su representación en forma de tabla el análisis de esa correspondencia en términos de función es por su parte mucho más delicado pues está implica no sólo la noción de relación numéricas sin igualmente la de consciente la de cociente de dimensiones   producto de media medida esta forma de relación consiste en una relación ternaria   entre 3 cantidades de las cuales eso es el producto de las otras dos tantos de plano numérico  como en  el plano dimensional.

Conclusión sobre la noción de dimensión

El análisis dimensional permite incluso establecer tal relación de una manera muy simple en efecto la utilización de un operador función para la solución de los problemas de la primera forma ISOMORFISMO  de medidas   permite encontrar la segunda forma producto de medida.

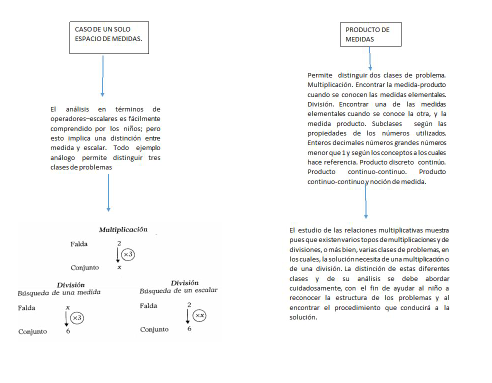
Clases de problemas de tipo multiplicativo  pueden extraer se numerosos clases de problemas según la forma de relación multiplicativa el carácter discreto o continuo de las cantidades intervienen las propiedades de los números utilizados etcétera

 Distinguir la las principales clases de problemas isomorfismo de medidas  el cual pon en juego 4 cantidad espero los problemas más simples se  sabe que una de estas es igual a 1 hay entonces grandes clases de problemas según   incógnita  sea  alguna de las otras tres cantidades.

Multiplicación. División búsqueda del valor unitario. División búsqueda de  la cantidad de unidades. Cada una de las clases se subdivide en numerosas subclases Multiplicación.

CASO DE UN SOLO ESPACIO DE MEDIDAS. El análisis en términos de operadores – escalares es fácilmente comprendido por los niños; pero esto implica una distinción entre medida y escalar.  Todo  ejemplo análogo permite distinguir tres clases de problemas 

 PRODUCTO DE MEDIDAS. Permite  distinguir dos clases de problema. Multiplicación. Encontrar la medida-producto cuando se conocen las medidas elementales. División. Encontrar una de las medidas elementales cuando se conoce la otra, y la medida producto. Subclases  según las propiedades de los números utilizados. Enteros decimales números grandes números menor que 1 y según los conceptos a los cuales hace referencia. Producto discreto  continúo. Producto continuo -continuo. Producto continuo-continuo y noción de medida.

^{ANÁLISIS DE LA CUARTA UNIDAD.}

^{Para que los niños aprendan la multiplicación y división tienen que reflexionar.}

^{La multiplicación es una suma iterada. hay dos tipos de problemas los de una relación proporcional los cuales son mas adecuados para que los niños empiecen a trabajar sobre ellos. Y otro aquellos en los que se multiplican las medidas de dos magnitudes para obtener una tercera. Es importante que los alumnos encentren dos propiedades  de la multiplicación; la conmutativa y la distributiva.}

^{La división es un reparto.}

^{Hay dos tipos de problemas de división; la tasativa o agrupamiento y de reparto, los cuales se pueden utilizar para que los niños empecen a trabajar con la división. También esta la división como sustracción iterada, con resto, con uno y con cero.}

los alumnos deben de darse cuenta de las propiedades de la división; cuando el dividendo aumenta en la misma cantidad y el divisor es el mismo, el cociente aumenta de uno en uno. Cuando el dividendo aumenta en la misma cantidad y el divisor aumenta de uno en uno, el cociente es el mismo, relación cociente-dividendo.