1. Preguntas del plan vigente para la educación básica

A)¿Cuáles son las características que determina el enfoque?

En la educación básica, la resolución de problemas es tanto una meta de aprendizaje como un medio para aprender contenidos matemáticos y fomentar el gusto con actitudes positivas hacia su estudio.

En el primer caso, se trata de que los estudiantes usen de manera flexible conceptos, técnicas, métodos o contenidos en general, aprendidos previamente; y en el segundo, los estudiantes desarrollan procedimientos de resolución que no necesariamente les han sido enseñados con anterioridad.

En ambos casos, los estudiantes analizan, comparan y obtienen conclusiones con ayuda del profesor; defienden sus ideas y aprenden a escuchar a los demás; relacionan lo que saben con nuevos conocimientos, de manera general; y le encuentran sentido y se interesan en las actividades que el profesor les plantea, es decir, disfrutan haciendo matemáticas

La resolución de problemas se hace a lo largo de la educación básica, aplicando contenidos y métodos pertinentes en cada nivel escolar, y transitando de planteamientos sencillos a problemas cada vez más complejos. Esta actividad incluye la modelación de situaciones y fenómenos, la cual no implica obtener una solución.

Es por ello que la evaluación no debe circunscribirse a la aplicación de exámenes en momentos fijos del curso, sino que debe ser un medio que permita al profesor y al estudiante conocer las fortalezas y debilidades surgidas en el proceso de aprendizaje Mediante actividades que utilizan herramientas tecnológicas es posible promover en los estudiantes la exploración de ideas y conceptos matemáticos, así como el análisis y modelación de fenómenos y situaciones problemáticas. Las herramientas de uso más frecuente en el diseño de actividades para el aprendizaje en matemáticas son las hojas electrónicas de cálculo, los manipuladores simbólicos y los graficadores

B) ¿Cuál es el campo de la formación que define las matemáticas en la educación?

 
Para su estudio, este espacio curricular se organiza en tres ejes temáticos y doce temas:

Número, álgebra y variación

Número

Adición y sustracción

Multiplicación y división

Proporcionalidad

Ecuaciones

Funciones

Patrones, figuras geométricas y expresiones equivalentes

Forma, espacio y medida

Ubicación espacial

Figuras y cuerpos geométricos

Magnitudes y medidas

Análisis de datos

Estadística

Probabilidad

C)¿Cuál es el perfil de egreso al termino de cada  nivel educativo de acuerdo al ámbito de pensamiento matemático?

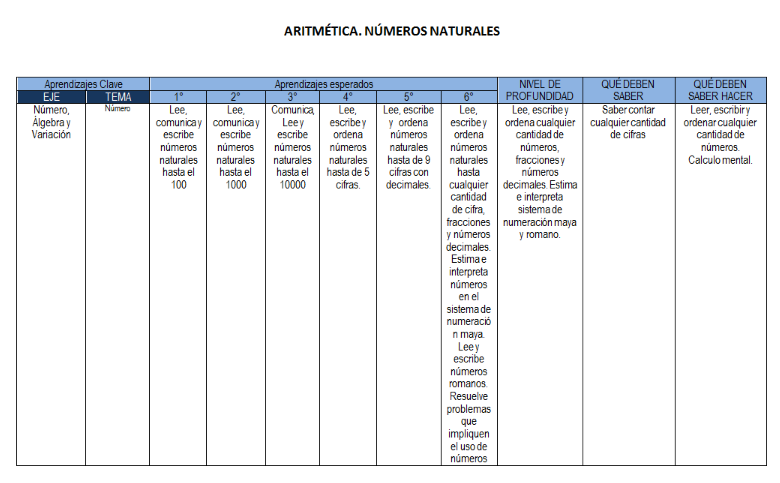
Aprendizajes esperados 1

• Lee, escribe y ordena números naturales hasta 100.

Comunica, lee, escribe y ordena números naturales hasta 1000

• Resuelve problemas de suma y resta con números naturales hasta 1000. Usa el algoritmo convencional para sumar.

• Calcula mentalmente sumas y restas de números de dos cifras, dobles de números de dos cifras y mitades de números pares menores que 100.

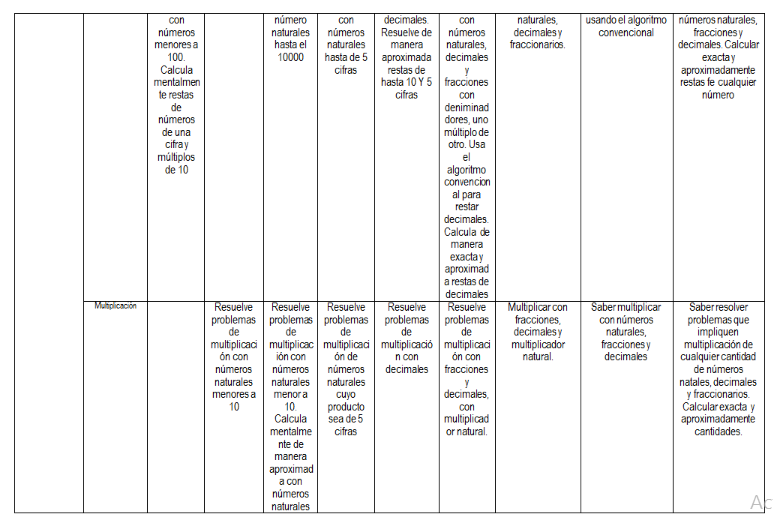
Resuelve problemas de multiplicación con números naturales menores que 10.

Aprendizaje esperado: 2

• Lee, escribe y ordena números naturales hasta 1000.

Aprendizajes esperados: 3

• Lee, escribe y ordena números naturales hasta 10000.
• Usa fracciones con denominador dos, cuatro y ocho para expresar relaciones parte-todo, medidas y resultados de repartos.

Aprendizajes esperados 4

• Lee, escribe y ordena números naturales hasta de cinco cifras...
• Usa fracciones con denominadores hasta 12 para expresar relaciones parte-todo, medidas, y resultados de repartos.

Aprendizajes esperados 5

• Lee, escribe y ordena números naturales hasta de nueve cifras y decimales.
• Ordena fracciones con denominadores múltiplos.

Aprendizajes esperados 6

• Lee, escribe y ordena números naturales de cualquier cantidad de cifras, fracciones y números decimales.
• Estima e interpreta números en el sistema de numeración maya.
• Lee y escribe números romanos.
• Resuelve problemas que impliquen el uso de números enteros al situarlos en la recta numérica, compararlos y ordenarlos.

2. PERFIL DE EGRESO POR NIVEL EDUCATIVO

3. PERFIL DE EGRESO EDUCACIÓN BÁSICA.

A) ¿Cuáles son los rasgos del perfil de egreso y los propósitos que propone el plan y programas para la educación básica?

R: 1) Se comunica con confianza y eficacia, Utiliza su lengua materna para comunicarse con eficacia, respeto y seguridad en distintos contextos con múltiples propósitos e interlocutores

2) Fortalece su pensamiento matemático, Amplía su conocimiento de técnicas y conceptos matemáticos para plantear y resolver problemas con distinto grado de complejidad, así como para modelar y analizar situaciones. Valora las cualidades del pensamiento matemático.

3) Gusta de explorar y comprender el mundo natural y social, Identifica una variedad de fenómenos del mundo natural y social, lee acerca de ellos, se informa en distintas fuentes, indaga aplicando principios del escepticismo informado, formula preguntas de complejidad creciente, realiza análisis y experimentos

4) Desarrolla el pensamiento crítico y resuelve problemas con creatividad, Reflexiona sobre sus procesos de pensamiento, se apoya en organizadores gráficos (por ejemplo, tablas o mapas mentales) para representarlos y evalúa su efectividad.

5) Posee auto-conocimiento y regula sus emociones, Asume responsabilidad sobre su bienestar y el de los otros, y lo expresa al cuidar su cuerpo, su mente y las relaciones con los demás

6) Tiene iniciativa y favorece la colaboración, Reconoce, respeta y aprecia la diversidad de capacidades y visiones al trabajar de manera colaborativa. Tiene iniciativa, emprende y se esfuerza por lograr proyectos personales y colectivos.

7) Asume su identidad, favorece la interculturalidad y respeta la legalidad, Se identifica como mexicano. Reconoce la diversidad individual, social, cultural, étnica y lingüística del país, y tiene conciencia del papel de México en el mundo.

8) Aprecia el arte y la cultura, Experimenta, analiza y aprecia distintas manifestaciones artísticas. Identifica y ejerce sus derechos culturales.

9) Cuida su cuerpo y evita conductas de riesgo, Activa sus destrezas motrices y las adapta a distintas situaciones que se afrontan en el juego y el deporte escolar

10) Muestra responsabilidad por el ambiente, Promueve el cuidado del medio ambiente de forma activa

11) Emplea sus habilidades digitales de manera pertinente, Compara y elige los recursos tecnológicos a su alcance y los aprovecha con una multiplicidad de fines.

Propósitos generales

1. Concebir las matemáticas como una construcción social en donde se formulan y argumentan hechos y procedimientos matemáticos.

2. Adquirir actitudes positivas y críticas hacia las matemáticas: desarrollar confianza en sus propias capacidades y perseverancia al enfrentarse a problemas; disposición para el trabajo colaborativo y autónomo; curiosidad e interés por emprender procesos de búsqueda en la resolución de problemas.

3. Desarrollar habilidades que les permitan plantear y resolver problemas usando herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.

Propósitos para la educación primaria

1. Utilizar de manera flexible la estimación, el cálculo mental y el cálculo escrito en las operaciones con números naturales, fraccionarios y decimales.

2. Identificar y simbolizar conjuntos de cantidades que varían proporcionalmente, y saber calcular valores faltantes y porcentajes en diversos contextos.

3. Usar e interpretar representaciones para la orientación en el espacio, para ubicar lugares y para comunicar trayectos.

4. Conocer y usar las propiedades básicas de triángulos, cuadriláteros, polígonos regulares, círculos y prismas.

5. Calcular y estimar el perímetro y el área de triángulos y cuadriláteros, y estimar e interpretar medidas expresadas con distintos tipos de unidad.

6. Buscar, organizar, analizar e interpretar datos con un propósito específico, y luego comunicar la información que resulte de este proceso.

7. Reconocer experimentos aleatorios y desarrollar una idea intuitiva de espacio maestral.

B) ¿Cuál es el campo de formación que define las matemáticas en la educación básica?

Número, álgebra y variación

 Numero

 Adicción y sustracción

 Multiplicación y división

 Proporcionalidad

 Ecuaciones

 Funciones

 Patrones, figuras geométricas y expresiones equivalentes

Forma, espacio y medida

 Ubicación espacial

 Figuras y cuerpos geométricos

 Magnitudes y medidas

Análisis de datos

 Estadística

 Probabilidad

C) ¿Cuál es el perfil de egreso al término de cada nivel educativo de acuerdo en al ámbito de pensamiento matemático?

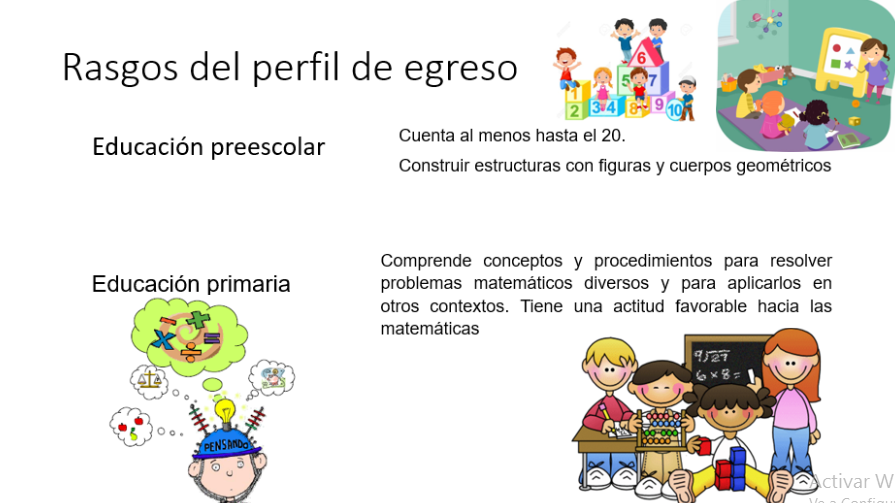
Al término de la educación preescolar

 Cuenta al menos hasta el 20. Razona para solucionar problemas de cantidad, construir estructuras con figuras y cuerpos geométricos, y organizar información de formas sencillas (por ejemplo, en tablas).

Al término de educación primaria

 Comprende conceptos y procedimientos para resolver problemas matemáticos diversos y para aplicarlos en otros contextos. Tiene una actitud favorable hacia las matemáticas

Al término de educación secundaria

 Amplía su conocimiento de técnicas y conocimientos matemáticos para ampliar y resolver problemas con distinto grado de complejidad,así como para modelar y analizar situaciones. Valora las cualidades del pensamiento matemático

Al término de la educación media superior

 Construye e interpreta situaciones reales, hipotéticas o formales que requieren la utilización del pensamiento matemático. Formula y resuelve problemas, aplicando diferentes enfoques.

3. Enfoque

4. Orientaciones didácticas 

5. Preguntas de orientaciones didácticas 

¿En qué consisten las orientaciones didácticas?

Aprender matemáticas es importante para aprender las siguientes metas:

 comprender la situación implicada en un problema. Representa que los alumnos comprendan a fondo el problema e identifiquen la información esencial para resolverlo. Es conveniente averiguar como analizar la información que deben de manera oral o escrita.

 Los alumnos proponen el camino a seguir. Tienen la posibilidad de: compartir ideas, abra acuerdos y desacuerdos, se expresaran con libertad y podrán reflexionar. El papel del docente es propiciar un diálogo productivo y no ofrecer soluciones .

 Trabaja en equipo. Esta estrategia afecte a los alumnos la posibilidad de expresar sus ideas y enriquecerlos con las opciones de los demás, desarrollar una actitud de colaboración y la habilidad para fundamentar sus argumentos. El maestro debe insistir en que todos los integrantes asuman la responsabilidad de resolver la tarea, no de manera individual si no de colectiva.

 Manejo adecuado del tiempo. Los alumnos resuelven problemas con sus propios medios, discuten y analizan sus procedimientos y sus resultados implican más tiempo. Si ellos comprenden lo que estudian, alcanzarán mejores resultados. Es indispensable prender tiempo para analizar lo que producen aclarar ideas, aportar información, explicación necesarias, tiempo para formar conocimiento en los problemas.

 Diversificar el tipo de problema. Es favorable es la planificación actitudes adicionales para aquellos alumnos que puedan enfrentar situaciones más complejas o para los que necesiten apoyo para comprender los conceptos matemáticos.

 Compartir experiencias con otros profesores. Será de gran ayuda que los maestros compartan experiencias entre ellas entorno al estudio de las matemáticas, pues sean estás exitosas o no, les permitirán mejorar permanentemente su trabajo.

6. Sugerencias de evaluación 

7. Preguntas de sugerencias de evaluación 

¿Cuál es el sustento teórico de las sugerencias de evaluación?

Tiene un enfoque formativo porque se centra en los procesos de aprendizaje y da seguimiento al progreso de los alumnos. Los errores de los alumnos son una oportunidad de aprendizaje para ellos y también para el maestro, en la medida en que estos se analicen, discutan y se tomen como base para orientar estrategias de aprendizaje.

 De resolver problemas con ayuda a solucionarlos autónoma-mente Trabajo de manera autónoma de principio a fin obteniendo resultados correctos.

 De la justificación pragmática al uso de propiedades. Interacción entre alumnos, objeto de conocimiento y maestro, generando la explicación de procedimientos y resultados.

 De los procedimientos informales a los procedimientos expertos. Los alumnos usan procedimientos informales, y es tarea del maestro que dichos procedimientos evolucionen hacia otros cada vez más eficaces.

8. Aprendizajes

9. PRESENTACIÓN 

ANÁLISIS DE LA PRIMERA UNIDAD.

En esta primera unidad se aprendieron los aprendizajes esperados a nivel básico primaria y aprendizajes esperados por nivel educativo , así como el enfoque pedagógico que es a través de la resolución de problemas, las orientaciones didácticas nos permiten tener una idea al maestro  sobre como analizan la información los alumnos, así como trabajo en equipo. las sugerencias de evaluación nos permiten ver algunos aspectos que se pueden considerar para una evaluación formativa.