1. Actividad orden-conteo

Dos procedimientos fundamentales asociados al número: agregar y completar, que son antecedentes no formales para las operaciones de suma y resta.

El objeto de consideración o no en la clase, plantean la percepción de totales y partes que los forman, sugieren que los números no son monolíticos, que se pueden descomponer en muchas formas. Estas percepciones son necesarias para la construcción de la noción de número y que el número conlleva en sí mismo las operaciones aritméticas

En el conjunto de los números naturales para todo número natural N el que le sigue es N+1 y se llama el sucesor de N. Y de N se dice que es el antecesor de N+1.

El conjunto o los conjuntos son colecciones de cosas y cada una de ellas es un elemento del conjunto. Contar una colección de objetos es algo más que establecer una correspondencia uno a uno entre una secuencia inicial de los números naturales y los elementos de la colección

a) De acuerdo con la información que presenta la guía enuncie las lecturas que puede darle a la Fig. 1.

Los pajaritos se ubican en un espacio formado por dos conjuntos de cinco troncos iguales uniformemente espaciados, en total diez troncos. Al “leer” las ilustraciones de arriba hacia abajo se observa la secuencia 1, 2, 3, 4 y 5. Mediante las imágenes se pide a los alumnos que registren sus respuestas en los cuadros en blanco.

Pero también pueden mirar invirtiendo el recorrido (5, 4, 3, 2 y 1) para completar los troncos vacíos y notar, de abajo hacia arriba, que faltan 5, 6, 7, 8 y 9 pajaritos. En cada imagen de troncos y pajaritos hay

Troncos con y sin pajaritos (sugiere 5=5+0;

4=4+0, etc.) Unos troncos chicos y otros grandes

• Hay manzanas, pero una es roja y otra verde

(Sugiere 2=1+1).

• Hay cinco pelotas, tres rosas y dos verdes

(Sugiere 5=3+2). Cuatro dentro del canasto y una fuera

• Hay cuatro lápices, tres rojos y uno azul

(Sugiere 4=3+1).dos chicos y dos grandes

b) ¿A qué nos inducen las imágenes como antecedentes no formales para las operaciones de suma y resta?

la noción de que los números se pueden componer y descomponer de distintas maneras a través de procedimientos que les son inherentes(esencial y permanente).

c) ¿Qué característica presenta la representación gráfica?

es que los conjuntos no son del todo homogéneos, presentan cualidades que permiten distinguir sus elementos

d) ¿En qué radica la importancia de la secuencia de los pajaritos?

radica en que introduce al niño en el “arte de contar”, de agregar y completar, que podemos construir un número a partir de otros. Esto permite introducir las nociones no formales de suma y resta sin necesidad de disponer de dos números, basta con uno que pueda descomponerse,

2.  Actividades que se sugieren para los futuros docentes

1.¿Cuál es la intención didáctica de presentar los 10 troncos de la ilustración en esta página distribuidos en dos grupos de 5 troncos?

Ver que el niño pueda comprar los elementos de los conjuntos así como clasificar los tamaños de cada tronco.

Ver en que posición se encuentra cada pajarito

2.¿Cuáles son las ventajas didácticas que ofrece el hecho de usar colecciones no homogéneas en esta lección?

Realizar comparaciones entre las distintas características (principio de abstracción) de los objetos o imágenes.

Tener en cuenta las distintas formas en las que se puede impartir el tema de orden y conteo.

3. ¿Cuáles serían las limitaciones didácticas si sólo se emplearan colecciones homogéneas?

No se podría hacer comparaciones entre los distintos elementos y conjuntos ya que serían iguales.

Algunos niños no comprenderían como comprar.

3.CONCEPTOS DE LA TSD.

¿Cuáles son las dos posiciones epistemológicas de las que parte la didáctica de las matemáticas de la escuela francesa?

La identificación de la interpretación de fenómenos y procesos, objeto de interés supone el desarrollo de un cuerpo teórico, y no puede realizarse a observaciones a partir de experiencias. La convicción de que ese cuerpo teórico debe ser específico del saber matemático y no puede provenir de la simple aplicación de la teoría.

¿Cómo se concibe el aprendizaje en la teoría de situaciones didácticas?

Concepción constructivista. El alumno aprende adaptándose a un medio; este saber fruto de la adaptación alumno se manifiesta por las respuestas nuevas que son la prueba del aprendizaje.

¿Cuál es la diferencia entre una situación didáctica y una a-didáctica?

La primera es un conjunto de relaciones entre el alumno, un medio y un sistema educativo (maestro). En la segunda los conocimientos se ponen en práctica y se sanciona las decisiones que toma el alumno.

¿Cuáles son y en que consisten los aspectos que definen a una situación a-

didáctica?

La necesidad al conocimiento a que se apunta, es necesario para resolución de ciertos problemas. Sanción, el alumno interactúa con un medio que le ofrezca información sobre su producción (que el alumno juzgue sus resultados). No intervención, los alumnos deben encontrar por si mismos relaciones entre sus elecciones y resultados que obtienen.

¿Cuál es la intervención del maestro en una situación a-didáctica?

El alumno acepta la responsabilidad de una situación de aprendizaje.

¿Qué es una variable didáctica y como puede ser utilizada?

Son sujeto teórico cuya finalidad es estudiar el conjunto de condiciones y relaciones propias del conocimiento bien determinado. Puede utilizar valores que permitan al alumno comprender y resolver la situación con sus conocimientos previos, y luego hacerle afrontar la construcción de un conocimiento fijando un nuevo valor de una variable.

¿En qué consiste la institucionalización?

Define las relaciones que pueden tener los comportamientos o producciones ¨libres¨ del alumno con el saber cultural o científico y con el proyecto didáctico.

4.Mapa conceptos básicos.

5. VÍDEO 1

a) Explique su propia idea de lo que podrían hacer los niños para solucionar la situación planteada.

El alumno podría dividir y multiplicar

b) ¿Cómo inicia la clase el maestro, y en general que rol juega en los distintos momentos de la clase.?

Plantea el problema tomando en cuenta que todos los alumnos lo entiendan (situación de acción, el alumno entra en contacto con el problema) Resolución del problema El rol que juega es importante ya que deja que los alumnos manejen un enfoque constructivista, el sólo es una guía para los alumnos, realiza cuestiones para hacer comprobaciones, criterio de no intervención los alumnos deben encontrar por si mismos relaciones entre sus elecciones y resultados

c) La importancia que representa el momento de la confrontación de resultados (para maestro y alumnos)

El maestro verificó las diferentes variables posibles para el resultado con anterioridad.En esta etapa se lleva a cabo es aspecto didáctico de institucionalización ya que el maestro hace una reflexión y comparación entre las diferentes formas de llevar al resultado. La sanción, el alumno ve la información que le ofrece sus resultados ( el alumno juzga sus resultados)

d) Las acciones que realiza el maestro ante los errores que cometen los alumnos.

Deja que con la ayuda de sus compañeros los que tienen errores se den cuenta por si solos con el fin de no evidenciar a ninguno.Conoce los resultados que obtuvieron los alumnos.Ve los distintos procedimientos para llegar al resultado Validación: los alumnos están de acuerdo que hay diferentes procedimientos para llegar al resultado, explicación de lo aprendido.

6.VÍDEO 2

a) Identifica la manera en que el profesor presenta el problema y explica su intención y el propósito de la actividad de enseñanza, los aprendizajes que espera que logren los alumnos.

Clase experimental: El profesor presenta unos cuadros de papel en la cual por la parte de atrás tiene el número, el único número que se ve es el resultado de la resta. La intención del maestro es que los alumnos tienen que averiguar la ecuación de la resta que conduzca al resultado (tres). Los estudiantes encontraran ciertas reglas ocultas en las respuestas de los problemas.

1: que el minuendo y es sustraendo se incrementan el uno.

2: hay los mismos números de ecuaciones como el valor de la diferencia

Si lo estuantes conocen las reglas pueden encontrar las diferentes maneras pueden encontrar todas las maneras posibles de minuendos y sustraendos más rápidamente

b) El profesor empezó la clase donde la diferencia es 3, ¿así lo planeó originalmente?, Explica por qué empezó con este caso.

Sí, porque así los alumnos lograrían darse cuenta del orden de las operaciones y las posibles formas de realizar las operaciones

c) Al inicio del video algunos niños se expresaron acerca del profesor ¿por qué los alumnos quieren a su profesor? ¿Puede explicar su respuesta a partir de la forma en que él prepara la clase?

Les gusta en muchas formas, es lindo, es buena persona, Si por que sus clases de matemáticas son divertidas e interesantes

d) En el video, un niño dijo: “Señor Seiyama, hay algo mal en las respuestas”. ¿Por qué dijo ese niño “hay algo mal en las respuestas” y muchos de sus compañeros estaban de acuerdo con él?

Se dio cuenta que había algo mal en las respuestas, no estaban en orden. Porque la mayoría se dio cuenta ya que el orden de las ecuaciones debería ser reacomodado

e) Aunado a estas respuestas relacione lo acontecido en el vídeo con la Teoría de Situaciones Didácticas. Planeación de la clase con la intención de que los alumnos aprendan las reglas del minuendo y sustraendo en esas restas.

Variables, distintas respuestas a la resta. Situación de acción: el alumno entra en contracto con el problema. Formulación: cuando el profesor la información par que el alumno pueda resolver el problema y cuando los alumnos participan para comparar resultados. Validación: explicación de lo aprendido Institucionalización: el profesor complementa y retroalimenta lo aprendido, formalizando los términos. Situación a didáctica: descubrimiento autónomo de las reglas. Necesidad de conocimiento: conocimientos previos para la realización de la resta Sanción, cuando el niño se dio cuenta del orden y lo corrige, cuando se da cuenta que el minuendo y el sustraendo va en orden.No intervención, los niños descubrieron por si solos.

7. Mapa aprender por medio de la resolución  de problemas.

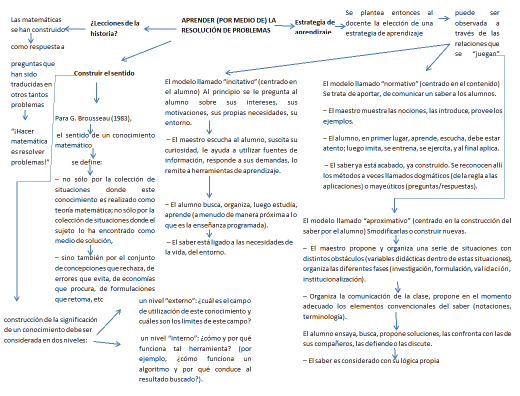
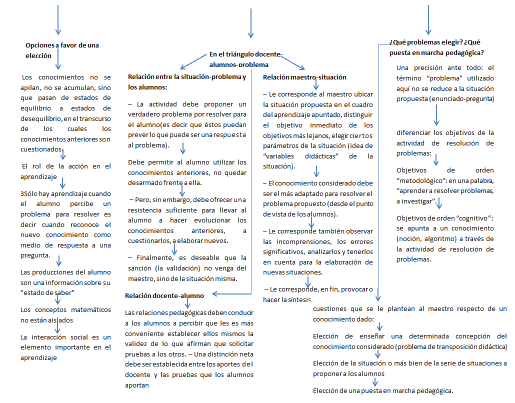
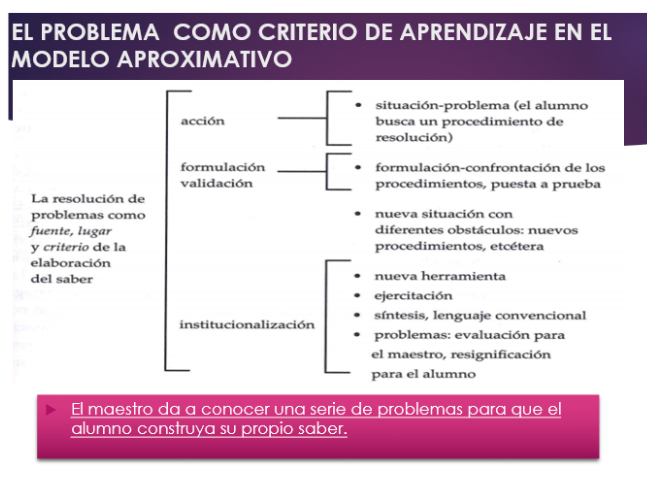
8. Presentación aprender por medio de la resolución de problemas. 

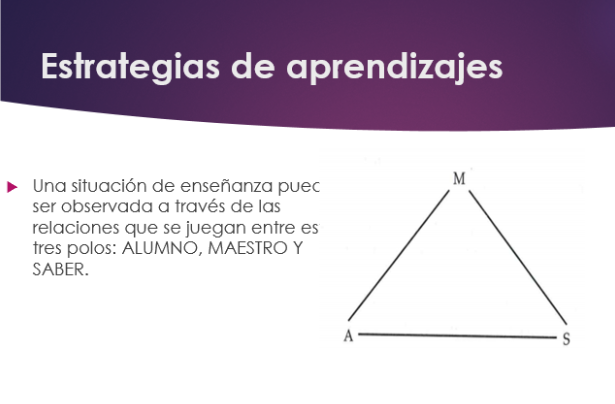
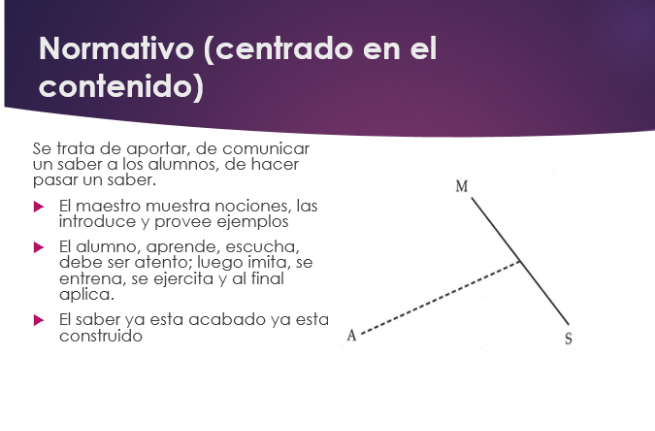
9.TRIPTICO 

10. PRÁCTICA GUÍA DE OBSERVACIÓN

Algunos de los aspectos que conviene que observen son los siguientes:

¿Cómo organizó el maestro al grupo para que realizaran la actividad?

Algunas actividades se realizaron de forma individual, otra en parejas y una de forma grupal.

¿En qué consistió la actividad planteada por el maestro?

La primera que fue individual los alumnos realizaron cálculo mental.

La segunda se realizó de forma individual fueron unas sumas con unidades y decenas.

La tercera fue grupal se les entregó la mitad de una hoja milimétrica y recortaron rectángulos con 10

cuadros dentro, después pasar algunos cuadros para formar decenas y ver cuanto era.

¿Cómo se usó el libro de texto gratuito?

Las sumas y la actividad de decenas y centenas venían en el libro de texto y de ahí tomo los ejemplos para poder impartir la clase.

¿Cuál fue la consigna (indicaciones) dada por el maestro?

Sacar la libreta para el cálculo mental, colocar la fecha del día de hoy, y colocar un listado de números del 1 al 5 como está en el pizarrón. La actividad de sumas ya estaba empezada cuando llegue así que no escuche indicaciones( primer día) Lupita, Ailyn repartan los libros de matemáticas, Diego, Luis repartan las libretas la maestra Rebe pasará a calificar la tarea y el cálculo mental mientras hacemos la actividad, coloquen la fecha mientras la maestra, Rebe reparte una hoja que se va a ocupar.

¿Cuál fue la actitud de los alumnos frente a la actividad?

Ellos estaban tranquilos y felices

¿Cuáles procedimientos o recursos fueron utilizados por los niños para realizar la

actividad?

Sumar con los dedos, hacían operaciones, colocaban palitos en la libreta, contaban los cuadritos, pedían ayuda a la maestra.

¿Qué hizo el maestro mientras los alumnos realizaban la actividad?

Les ayudaba si tenían dudas, calificar otras actividades, estaba en el teléfono, veía que todos los alumnos  estuvieran trabajando.

¿Cuál fue la actitud del maestro frente a las participaciones y respuestas de los

alumnos?

La muestra estaba feliz de que la mayoría de los alumnos participarán en los ejercicios y a la hora de ver los errores.

¿Cómo se validaron los procedimientos y respuestas de los alumnos?

La muestra paso a algunos alumnos que querían participar para dar respuesta la actividad y si estaban mal no se los decía como tal sino que pedía que le ayudarán los compañeros.

¿Qué contenidos matemáticos se trabajaron al realizar la actividad y a qué eje temático

corresponden?

Número, álgebra y variación.

Número, adición y sustracción.

¿Qué aprendieron los alumnos al realizar la actividad?

11.Conclusión de la práctica.

De acuerdo con la teoría de situaciones didácticas pudimos rescatar las siguientes

teorías y aspectos en las escuelas.Teoría didáctica: cuando el maestro planificó su clase tomando en cuenta los conocimientos previos de los alumnos para construir nuevos, con distintos materias didácticos (bate lenguas, colores, hojas y tarjetas).  Dentro de esta teoría identificamos las siguientes situaciones: Acción, cuando el maestro da por primera ves el problema y los alumnos entran en contacto con el, enfrentamiento a la resolución del problema. Formulación, los maestros interactúan con los alumnos así como alumnos con alumnos. Validación, cuando comparten sus respuestas con todo el grupo tomando en cuenta los diferentes procedimientos por los cuales se puede llegar al resultado(variables). No intervención, el maestro hace que los alumnos se mantienen concentrados en el problema y cuando se distraen hace que vuelvan a el.

Yo creo que en la mayoría de los salones en las dos escuelas se toma en cuenta la teoría de situaciones didácticas ya que es el sustento para llevar a cabo el enfoque, sin embargo consideró que deberían utilizar más la devolución para que los alumnos puedan resolver los problemas solos, ya que por lo observado el maestro ayudaba bastante a los alumnos dándolo las respuestas o la forma en como se tiene que hacer.

12. Vídeo de la clase de matemáticas primer año.

De acuerdo con el vídeo puede observar algunos aspectos como los siguientes

Teoría didáctica, el maestro utilizó una caja y dentro de ella tenía 30 tapas para

que los alumnos comprendieran el problema.

El maestro dio instrucciones y luego dio el problema así sucede la situación de acción ya que los alumnos entran en contacto con el problema cuando él maestro lea dice que encuentren cuantas tapan quedan en la caja después de que un compañero saco 10 tapas y así empieza la resolución del problema. Devolución, los alumnos realizan el problema solos aceptado la responsabilidad de resolverlo. La no intervención, el maestro hace que los alumnos que están trabajando en equipo estén concentrados en el problema. Los alumnos encuentran varias formas de resolver el problema (variables previstas por el profesor) utilizando representaciones irónicas Formulación, el maestro interactúa con los alumnos preguntando cosas sencillas Y los alumnos interactúan entre ellos para ver como lo van a resolver y si están de acuerdo con el resultado Validación, cuando del maestro pregunta si están de acuerdo de que el resultado es 20 y todos dicen que si. Institucionalización, el maestro completa y retroalimenta lo aprendido sacando y contando las tapas que quedaron dentro de la caja confirmando el resultado de todos.

Yo creo que el maestro si utiliza algunos aspectos de la teoría de situaciones didácticas ya que es fundamental para el enfoque porque las matemáticas están en la vida diaria en procesos sencillos como ir a comparar. Hacer operaciones pequeñas con la mente. Aprender a sumar cantidades menores y mayores de 100 Comprendieron mejor el como se completa una decena. Su opinión general sobre el desarrollo de la clase, el papel del maestro y de los alumnos. Yo creo por lo que puede observar los tres días que el desarrollo de la clase se fue dañado conforme los alumnos iban comprendiendo lo que estaban realizando, en mi opinión la maestra es buena y paciente con los alumnos para que puedan comprender lo que hacen, los alumnos participan con gran entusiasmo sólo que se distraen con gran facilidad y eso hace que se desvíe un poco la clase sin embargo la profesora trata de que todos estén atentos en la clase.

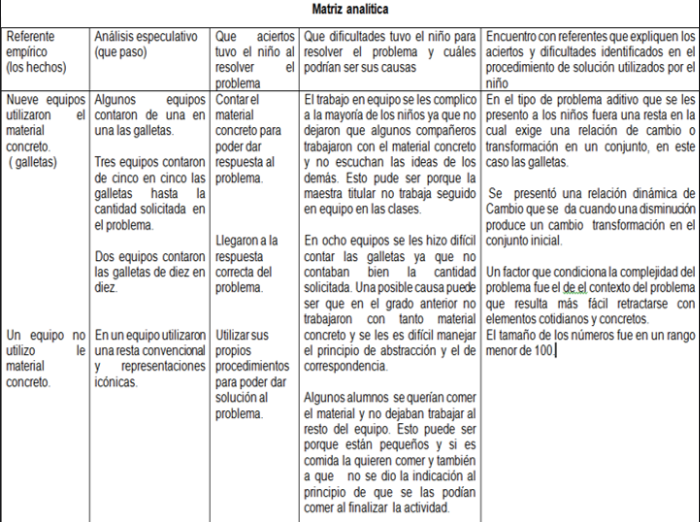
13. Matriz analítica.

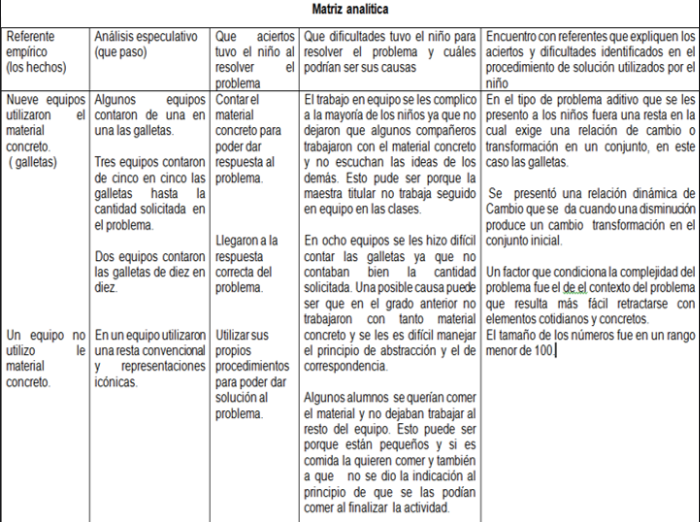
14. Presentación proceso de aprendizaje del niño respecto a la suma y resta 

ANÁLISIS DE LA TERCERA UNIDAD.

Al momento de querer introducir la suma y la resta no se tiene que empezar con un algoritmo, si no que se tiene que introducir a través de la resolución de problemas, esto permite que los niños estén más interesados pro resolver el problema. Al momento de empezar a resolver problemas de suma y resta es importante que los alumnos lo empiecen a realizar a través de material concreto.

La teoría de situaciones didácticas es el sustento para el enfoque pedagógico. Al momento de realizar una secuencia didáctica o planeación se tiene que tomar en cuenta  aspectos dicha teoría como son: situación de acción, situación de formulación y situación de validación. El modelo que se tiene que utilizar dentro de un aula es el modelo aproximativo que esta centrado en la construcción del saber por el alumno.

Hay diferentes tipos de problemas aditivos simples que se pueden utilizar para que el alumno trabaje, estos son; cambio, combinación, comparación  e igualación. Dentro de estos hay dos tipos de de relación; dinámica y estática.